
【题目】如图,三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC,AA1=2,AB=BC=1,∠ABC=90°,外接球的球心为O,点E是侧棱BB1上的一个动点.有下列判断: ①直线AC与直线C1E是异面直线;②A1E一定不垂直于AC1;③三棱锥E﹣AA1O的体积为定值;④AE+EC1的最小值为2 ![]() .
.
其中正确的个数是( )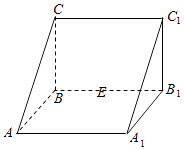
A.1
B.2
C.3
D.4
【答案】C
【解析】解:如图,
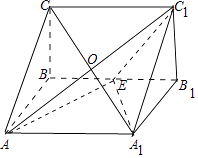
对于①,∵直线AC经过平面BCC1B1内的点C,而直线C1E在平面BCC1B1内不过C,∴直线AC与直线C1E是异面直线,故①正确;
对于②,当E与B重合时,AB1⊥A1B,而C1B1⊥A1B,∴A1B⊥平面AB1C1,则A1E垂直AC1,故②错误;
对于③,由题意知,直三棱柱ABC﹣A1B1C1的外接球的球心为O是AC1 与A1C 的交点,则△AA1O的面积为定值,由BB1∥平面AA1C1C,∴E到平面AA1O的距离为定值,∴三棱锥E﹣AA1O的体积为定值,故③正确;
对于④,设BE=x,则B1E=2﹣x,∴AE+EC1= ![]() .由其几何意义,即平面内动点(x,1)与两定点(0,0),(2,0)距离和的最小值知,其最小值为2
.由其几何意义,即平面内动点(x,1)与两定点(0,0),(2,0)距离和的最小值知,其最小值为2 ![]() ,故④正确.
,故④正确.
∴正确命题的个数是3个.
故选:C.
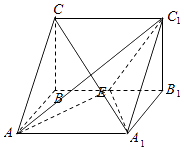
【考点精析】根据题目的已知条件,利用棱柱的结构特征的相关知识可以得到问题的答案,需要掌握两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形.


科目:高中数学 来源: 题型:
【题目】已知圆P过A(﹣8,0),B(2,0),C(0,4)三点,圆Q:x2+y2﹣2ay+a2﹣4=0.
(1)求圆P的方程;
(2)如果圆P和圆Q相外切,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资商到一开发区投资72万元建起一座蔬菜加工厂,第一年共支出12万元,以后每年支出增加4万元,从第一年起每年蔬菜销售收入50万元.设f(n)表示前n年的纯利润总和(f(n)=前n年的总收入﹣前n年的总支出﹣投资额).
(1)该厂从第几年开始盈利?
(2)若干年后,投资商为开发新项目,对该厂有两种处理方法:①年平均纯利润达到最大时,以48万元出售该厂;②纯利润总和达到最大时,以16万元出售该厂,问哪种方案更合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知首项为1的数列{an}的前n项和为Sn , 若点(Sn﹣1 , an)(n≥2)在函数y=3x+4的图象上. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=log2 ![]() ,且bn=2n+1cn , 其中n∈N* , 求数列{cn}的前前n项和Tn .
,且bn=2n+1cn , 其中n∈N* , 求数列{cn}的前前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在公差大于0的等差数列{an}中,2a7﹣a13=1,且a1 , a3﹣1,a6+5成等比数列,则数列{(﹣1)n﹣1an}的前21项和为( )
A.21
B.﹣21
C.441
D.﹣441
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x﹣3y﹣6=0,点T(﹣1,1)在AD边所在直线上. (Ⅰ)求AD边所在直线的方程;
(Ⅱ)求矩形ABCD外接圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
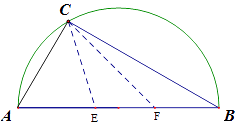
【题目】如图,有一直径为8米的半圆形空地,现计划种植果树,但需要有辅助光照.半圆周上的C处恰有一可旋转光源满足果树生长的需要,该光源照射范围是 ![]() ,点E,F在直径AB上,且
,点E,F在直径AB上,且 ![]() .
. 
(1)若 ![]() ,求AE的长;
,求AE的长;
(2)设∠ACE=α,求该空地种植果树的最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=sin(2x+ ![]() )的图象向右平移
)的图象向右平移 ![]() 个最小正周期后,所得图象对应的函数为( )
个最小正周期后,所得图象对应的函数为( )
A.y=sin(2x﹣ ![]() )
)
B.y=sin(2x﹣ ![]() )
)
C.y=sin(2x﹣ ![]() )
)
D.y=sin(2x+ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在△ABC中,A,B的坐标分别为(-1,2),(4,3),AC的中点M在y轴上,BC的中点N在x轴上.
(1)求点C的坐标;
(2)求直线MN的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com