解:(Ⅰ)由f'(x)=3x
2-4x-4=(3x+2)(x-2)=0,得
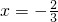
或2.
则x变化时,f′(x),f(x)的变化情况如下表:
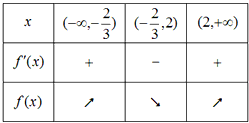
则f(x)的单调递增区间为
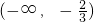
,(2,+∞),单调递减区间为
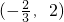
.
(Ⅱ)令g(x)=f(x)-f(a)-f'(a)(x-a),
则g'(x)=3x
2-4x-4-(3a
2-4a-4),记g'(x)=h(x),
因为当x>2时,h'(x)=6x-4>0,则h(x)在(2,+∞)单调递增,
又因为g'(a)=h(a)=0,
所以当2<x<a时,g'(x)<0,当x>a时,g'(x)>0,
所以g(x)在(2,a)递减,在(a,+∞)递增,又x≠a,
所以g(x)>g(a)=0成立,所以命题得证.
(Ⅲ)因为f(x)的单调递增区间为
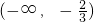
,(2,+∞),单调递减区间为
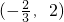
,且
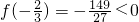
,
所以函数f(x)的零点x
0只有一个,且x
0>2,且对(-∞,x
0)内的任意实数x,都有f(x)<0,
因为f(α)>0=f(x
0),所以α>x
0>2,所以f'(α)=(3α+2)(α-2)>0,
在(Ⅱ)的结论中,取a=α,x=x
0,
则有f(α)+f'(a)(x
0-α)<f(x
0)=0,①
由
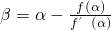
,得f(α)+f'(α)(β-α)=0,②
构造函数F(x)=f(α)+f'(α)(x-α),
则由①得F(x
0)<0,由②得F(β)=0,所以F(x
0)<F(β),
因为f'(α)>0,所以F′(x)=f'(α)>0,所以F(x)=f(α)+f'(α)(x-α)为增函数,
所以x
0<β,
因为F(α)=f(a)>0=F(β),所以β<α,
综上得x
0<β<α.
分析:(Ⅰ)求导数f′(x),解不等式f′(x)>0,f′(x)<0即可;
(Ⅱ)令g(x)=f(x)-f(a)-f'(a)(x-a),利用导数证明g
min(x)>0即可;
(Ⅲ)由函数极值可判断零点x
0的范围,再由f(α)>0可判断α与x
0的大小,由
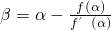
,得f(α)+f'(α)(β-α)=0,构造函数F(x)=f(α)+f'(α)(x-α),据F(x)的单调性及F(x
0)与F(β)的大小可判断βx
0的大小,从而可以得到答案.
点评:本题考查利用导数研究函数的单调性、函数极值,考查学生综合运用所学知识分析问题解决问题的能力,综合性强,能力要求高,难度较大.

 ,试探究实数α、β、x0的大小关系.
,试探究实数α、β、x0的大小关系.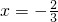 或2.
或2.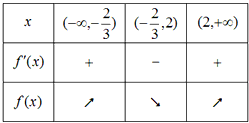
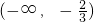 ,(2,+∞),单调递减区间为
,(2,+∞),单调递减区间为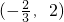 .
.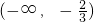 ,(2,+∞),单调递减区间为
,(2,+∞),单调递减区间为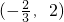 ,且
,且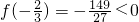 ,
,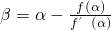 ,得f(α)+f'(α)(β-α)=0,②
,得f(α)+f'(α)(β-α)=0,②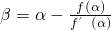 ,得f(α)+f'(α)(β-α)=0,构造函数F(x)=f(α)+f'(α)(x-α),据F(x)的单调性及F(x0)与F(β)的大小可判断βx0的大小,从而可以得到答案.
,得f(α)+f'(α)(β-α)=0,构造函数F(x)=f(α)+f'(α)(x-α),据F(x)的单调性及F(x0)与F(β)的大小可判断βx0的大小,从而可以得到答案.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<