
ЁОЬтФПЁПФГЪщЕъЯњЪлИеИеЩЯЪаЕФФГжЊУћЦЗХЦЕФИпШ§Ъ§бЇЕЅдЊОэЃЌАДЪТЯШФтЖЈЕФМлИёНјаа5ЬьЪдЯњЃЌУПжжЕЅМлЪдЯњ1ЬьЃЌЕУЕНШчБэЪ§ОнЃК
ЕЅМлxЃЈдЊЃЉ | 18 | 19 | 20 | 21 | 22 |
ЯњСПyЃЈВсЃЉ | 61 | 56 | 50 | 48 | 45 |
ЃЈ1ЃЉЧѓЪдЯњ5ЬьЕФЯњСПЕФЗНВюКЭyЖдxЕФЛиЙщжБЯпЗНГЬЃЛ
ЃЈ2ЃЉдЄМЦНёКѓЕФЯњЪлжаЃЌЯњСПгыЕЅМлЗўДгЃЈ1ЃЉжаЕФЛиЙщЗНГЬЃЌвбжЊУПВсЕЅдЊОэЕФГЩБОЪЧ14дЊЃЌ
ЮЊСЫЛёЕУзюДѓРћШѓЃЌИУЕЅдЊОэЕФЕЅМлгІЖЈЮЊЖрЩйдЊЃП
ЁОД№АИЁПЃЈ1ЃЉ![]() ;(2) ЕЅМлгІЖЈЮЊ23.5дЊЪБЃЌПЩЛёЕУзюДѓРћШѓ.
;(2) ЕЅМлгІЖЈЮЊ23.5дЊЪБЃЌПЩЛёЕУзюДѓРћШѓ.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉгЩЛиЙщжБЯпЗНГЬЕФЙЋЪНЧѓЕУ![]()
![]() ЃЌдйДњШыЙЋЪН
ЃЌдйДњШыЙЋЪН![]() ЧѓЕУa,зюжеЕУЕНБэДяЪНЃЛЃЈ2ЃЉЯШМЦЫуГіРћШѓЕФБэДяЪНz=ЃЈxЉ14ЃЉy=Љ4x2+188xЉ1848ЃЌдйЖдетИіЖўДЮКЏЪ§ЧѓЕУзюжЕМДПЩЁЃ
ЧѓЕУa,зюжеЕУЕНБэДяЪНЃЛЃЈ2ЃЉЯШМЦЫуГіРћШѓЕФБэДяЪНz=ЃЈxЉ14ЃЉy=Љ4x2+188xЉ1848ЃЌдйЖдетИіЖўДЮКЏЪ§ЧѓЕУзюжЕМДПЩЁЃ
ЃЈ1ЃЉ ![]()
![]() ИљОнЙЋЪНЕУЕН
ИљОнЙЋЪНЕУЕН![]()
ЫљвдyЖдxЕФЛиЙщжБЯпЗНГЬЮЊЃК ![]()
ЃЈ2ЃЉЛёЕУЕФРћШѓz=ЃЈxЉ14ЃЉy=Љ4x2+188xЉ1848ЃЌ
ЁпЖўДЮКЏЪ§z=Љ4x2+188xЉ1848ЕФПЊПкГЏЯТЃЌЁрЕБ![]() ЃЌzШЁзюДѓжЕЃЌ
ЃЌzШЁзюДѓжЕЃЌ
ЁрЕБЕЅМлгІЖЈЮЊ23.5дЊЪБЃЌПЩЛёЕУзюДѓРћШѓЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са![]() Тњзу
Тњзу![]() ЃЌ
ЃЌ ![]() ЃЌЦфжа
ЃЌЦфжа![]() .
.
ЃЈ1ЃЉЩш![]() ЃЌЧѓжЄЃКЪ§Са
ЃЌЧѓжЄЃКЪ§Са![]() ЪЧЕШВюЪ§СаЃЌВЂЧѓГі
ЪЧЕШВюЪ§СаЃЌВЂЧѓГі![]() ЕФЭЈЯюЙЋЪНЃЛ
ЕФЭЈЯюЙЋЪНЃЛ
ЃЈ2ЃЉЩш![]() ЃЌЪ§Са
ЃЌЪ§Са![]() ЕФЧА
ЕФЧА![]() ЯюКЭЮЊ
ЯюКЭЮЊ![]() ЃЌЪЧЗёДцдке§ећЪ§
ЃЌЪЧЗёДцдке§ећЪ§![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() Ждгк
Ждгк![]() КуГЩСЂЃЌШєДцдкЃЌЧѓГі
КуГЩСЂЃЌШєДцдкЃЌЧѓГі![]() ЕФзюаЁжЕЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФзюаЁжЕЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНќЦкжабыЕчЪгЬЈВЅГіЕФЁЖжаЙњЪЋДЪДѓЛсЁЗЛ№БщШЋЙњЃЌЯТУцЪЧзщЮЏЛсдкбЁАЮШќЪБЫцЛњГщШЁЕФ100УћбЁЪжЕФГЩМЈЃЌАДГЩМЈЗжзщЃЌЕУЕНЕФЦЕТЪЗжВМБэШчЯТЫљЪОЃК
зщКХ | Зжзщ | ЦЕЪ§ | ЦЕТЪ |
Ек1зщ |
|
| |
Ек2зщ |
| Ђй | |
Ек3зщ |
| 20 | Ђк |
Ек4зщ |
| 20 |
|
Ек5зщ |
| 10 |
|
КЯМЦ | 100 |
|
ЃЈ1ЃЉЧыЯШЧѓГіЦЕТЪЗжВМБэжаЂйЁЂЂкЮЛжУЕФЯргІЪ§ОнЃЌдйЭъГЩЦЕТЪЗжВМжБЗНЭМЃЈгУвѕгАБэЪОЃЉЃЛ
ЃЈ2ЃЉЮЊСЫФмбЁАЮГізюгХауЕФбЁЪжЃЌзщЮЏЛсОіЖЈдкБЪЪдГЩМЈИпЕФЕк3ЁЂ4ЁЂ5зщжагУЗжВуГщбљГщШЁ5УћбЁЪжНјШыЕкЖўТжУцЪдЃЌЧѓЕк3ЁЂ4ЁЂ5зщУПзщИїГщШЁЖрЩйУћбЁЪжНјШыЕкЖўТжУцЪдЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЧАЬсЯТЃЌзщЮЏЛсОіЖЈдк5УћбЁЪжжаЫцЛњГщШЁ2УћбЁЪжНгЪм![]() ПМЙйНјааУцЪдЃЌЧѓЃКЕк4зщжСЩйгавЛУћбЁЪжБЛПМЙй
ПМЙйНјааУцЪдЃЌЧѓЃКЕк4зщжСЩйгавЛУћбЁЪжБЛПМЙй![]() УцЪдЕФИХТЪ.
УцЪдЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=AsinЃЈx+ІеЃЉЃЈAЃО0ЃЌ0ЃМІеЃМІаЃЉЃЌxЁЪRЕФзюДѓжЕЪЧ1ЃЌЦфЭМЯѓОЙ§Еу ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓfЃЈxЃЉЕФНтЮіЪНЃЛ
ЃЈ2ЃЉвбжЊ ![]() ЃЌЧв
ЃЌЧв ![]() ЃЌ
ЃЌ ![]() ЃЌЧѓfЃЈІСЉІТЃЉЕФжЕЃЎ
ЃЌЧѓfЃЈІСЉІТЃЉЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌвбжЊЖЈЕуA(Ѓ4ЃЌ0)ЁЂC(4ЃЌ0)ЃЌАыОЖЮЊrЕФдВMЕФдВаФMдкЯпЖЮACЕФДЙжБЦНЗжЯпЩЯЃЌЧвдкyжсгвВрЃЌдВMБЛyжсНиЕУЕФЯвГЄЮЊ![]() r.
r.
(1)ЧѓдВMЕФЗНГЬЃЛЃЈ2)ЕБrБфЛЏЪБЃЌЪЧЗёДцдкЖЈжБЯпlгыЖЏдВMОљЯрЧаЃПШчЙћДцдкЃЌЧѓГіЖЈжБЯпlЕФЗНГЬЃЛШчЙћВЛДцдкЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдке§ЗНаЮ![]() жаЃЌ
жаЃЌ ![]() ЕФжаЕуЮЊЕу
ЕФжаЕуЮЊЕу![]() ЃЌ
ЃЌ ![]() ЕФжаЕуЮЊЕу
ЕФжаЕуЮЊЕу![]() ЃЌби
ЃЌби![]() НЋ
НЋ![]() ЯђЩЯелЦ№ЕУЕН
ЯђЩЯелЦ№ЕУЕН![]() ЃЌЪЙЕУУц
ЃЌЪЙЕУУц![]() Уц
Уц![]() ЃЌДЫЪБЕу
ЃЌДЫЪБЕу![]() ЮЛгкЕу
ЮЛгкЕу![]() ДІЃЎ
ДІЃЎ
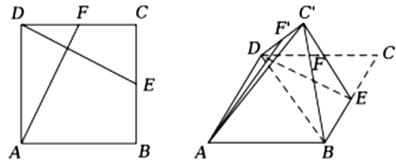
ЃЈЂёЃЉжЄУїЃК ![]() ЃЛ
ЃЛ
ЃЈЂђЃЉЧѓУц![]() гыУц
гыУц![]() ЫљГЩЖўУцНЧЕФе§ЯвжЕЃЎ
ЫљГЩЖўУцНЧЕФе§ЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхЦНУцЯђСПжЎМфЕФвЛжждЫЫуЁАЁбЁБШчЯТЃКЖдШЮвтЕФ ![]() ЃЌСю
ЃЌСю ![]() Ёб
Ёб ![]() =mq-npЃЌЯТУцЫЕЗЈДэЮѓЕФЪЧЃЈ ЃЉ
=mq-npЃЌЯТУцЫЕЗЈДэЮѓЕФЪЧЃЈ ЃЉ
A.Шє ![]() гы
гы ![]() ЙВЯпЃЌдђ
ЙВЯпЃЌдђ ![]() Ёб
Ёб ![]() =0
=0
B.![]() Ёб
Ёб ![]() =
= ![]() Ёб
Ёб ![]()
C.ЖдШЮвтЕФІЫЁЪRЃЌга ![]() Ёб
Ёб ![]() =
= ![]() Ёб
Ёб ![]() ЃЉ
ЃЉ
D.ЃЈ ![]() Ёб
Ёб ![]() ЃЉ2+ЃЈ
ЃЉ2+ЃЈ ![]() ЃЉ2=|
ЃЉ2=| ![]() |2|
|2| ![]() |2
|2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЃЌввСНЬЈЛњДВЭЌЪБЩњВњвЛжжСуМўЃЌЦфжЪСПАДВтЪджИБъЛЎЗжЃКжИБъДѓгкЛђЕШгк100ЮЊгХЦЗЃЌДѓгкЕШгк90ЧваЁгк100ЮЊКЯИёЦЗЃЌаЁгк90ЮЊДЮЦЗЃЌЯжЫцЛњГщШЁетСНЬЈГЕДВЩњВњЕФСуМўИї100МўНјааМьВтЃЌМьВтНсЙћЭГМЦШчЯТЃК
ВтЪджИБъ |
|
|
|
|
|
ЛњДВМз | 8 | 12 | 40 | 32 | 8 |
ЛњДВвв | 7 | 18 | 40 | 29 | 6 |
ЃЈ1ЃЉЪдЗжБ№ЙРМЦМзЛњДВЁЂввЛњДВЩњВњЕФСуМўЮЊгХЦЗЕФИХТЪЃЛ
ЃЈ2ЃЉМзЛњДВЩњВњвЛМўСуМўЃЌШєЪЧгХЦЗПЩгЏРћ160дЊЃЌКЯИёЦЗПЩгЏРћ100дЊЃЌДЮЦЗдђПїЫ№20дЊЃЛМйЩшМзЛњДВФГЬьЩњВњ50МўСуМўЃЌЧыЙРМЦМзЛњДВИУЬьЕФШеРћШѓЃЈЕЅЮЛЃКдЊЃЉЃЛ
ЃЈ3ЃЉДгМзЁЂввЛњДВЩњВњЕФСуМўжИБъдк![]() ФкЕФСуМўжаЃЌВЩгУЗжВуГщбљЕФЗНЗЈГщШЁ5МўЃЌДгет5МўжаШЮбЁ2МўНјаажЪСПЗжЮіЃЌЧѓет2МўЖМЪЧввЛњДВЩњВњЕФИХТЪ.
ФкЕФСуМўжаЃЌВЩгУЗжВуГщбљЕФЗНЗЈГщШЁ5МўЃЌДгет5МўжаШЮбЁ2МўНјаажЪСПЗжЮіЃЌЧѓет2МўЖМЪЧввЛњДВЩњВњЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕу![]() ЪЧдВ
ЪЧдВ![]() ЩЯЕФШЮвтвЛЕуЃЌЕу
ЩЯЕФШЮвтвЛЕуЃЌЕу![]() ЮЊдВ
ЮЊдВ![]() ЕФдВаФЃЌЕу
ЕФдВаФЃЌЕу![]() гыЕу
гыЕу![]() ЙигкЦНУцжБНЧЯЕЕФзјБъдЕуЖдГЦЃЌЯпЖЮ
ЙигкЦНУцжБНЧЯЕЕФзјБъдЕуЖдГЦЃЌЯпЖЮ![]() ЕФДЙжБЦНЗжЯпгыЯпЖЮ
ЕФДЙжБЦНЗжЯпгыЯпЖЮ![]() НЛгкЕу
НЛгкЕу![]() .
.
ЃЈ1ЃЉЧѓЖЏЕу![]() ЕФЙьМЃ
ЕФЙьМЃ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉШєЙьМЃ![]() гы
гы![]() жсе§АыжсНЛгкЕу
жсе§АыжсНЛгкЕу![]() ЃЌжБЯп
ЃЌжБЯп![]() НЛЙьМЃ
НЛЙьМЃ![]() гк
гк![]() СНЕуЃЌЧѓ
СНЕуЃЌЧѓ![]() УцЛ§ЕФШЁжЕЗЖЮЇ.
УцЛ§ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com