
【题目】已知向量 ![]() ,b(sinωx,0),且ω>0,设函数f(x)=(a+b)b+k.
,b(sinωx,0),且ω>0,设函数f(x)=(a+b)b+k.
(1)若f(x)的图像中相邻两条对称轴间的距离不小于 ![]() ,求ω的取值范围.
,求ω的取值范围.
(2)若f(x)的最小正周期为π,且当 ![]() 时,f(x)的最大值是2,求k的值.
时,f(x)的最大值是2,求k的值.
【答案】
(1)解:∵ ![]() ,
, ![]() (sinωx,0),
(sinωx,0),
∴ ![]() +
+ ![]() =(
=( ![]() cosωx+sinωx,sinωx),
cosωx+sinωx,sinωx),
∴f(x)= ![]() sinωxcosωx+sin2ωx+k
sinωxcosωx+sin2ωx+k
= ![]() sin2ωx﹣
sin2ωx﹣ ![]() cos2ωx+
cos2ωx+ ![]() +k
+k
=sin(2ωx﹣ ![]() )+
)+ ![]() +k,
+k,
由题意得:T= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ≥
≥ ![]() ,∴ω≤1,又ω>0,
,∴ω≤1,又ω>0,
则ω的取值范围0<ω≤1
(2)解:∵T=π,∴ ![]() =π,即ω=1,
=π,即ω=1,
∴f(x)=sin(2x﹣ ![]() )+
)+ ![]() +k,
+k,
∵ ![]() ,∴2x﹣
,∴2x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],
],
则当2x﹣ ![]() =
= ![]() ,即x=
,即x= ![]() 时,f(x)取得最大值,
时,f(x)取得最大值,
∴f( ![]() )=2,及sin(2×
)=2,及sin(2× ![]() ﹣
﹣ ![]() )+
)+ ![]() +k=2,
+k=2,
解得:k=1.
【解析】由 ![]() 和
和 ![]() 的坐标求出
的坐标求出 ![]() +
+ ![]() 的坐标,进而利用平面向量的数量积运算法则算出(
的坐标,进而利用平面向量的数量积运算法则算出( ![]() +
+ ![]() )
) ![]() 的值,把f(x)的解析式变形,再利用二倍角的正弦、余弦函数公式化简,从而利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,(1)找出ω的值,代入周期公式求出f(x)的周期,根据f(x)的图像中相邻两条对称轴间的距离不小于
的值,把f(x)的解析式变形,再利用二倍角的正弦、余弦函数公式化简,从而利用两角和与差的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,(1)找出ω的值,代入周期公式求出f(x)的周期,根据f(x)的图像中相邻两条对称轴间的距离不小于 ![]() ,得到周期的一半大于等于
,得到周期的一半大于等于 ![]() ,再由ω>0即可求出ω的取值范围;(2)由f(x)的最小正周期为π求出ω的值,代入f(x)的解析式,根据x的范围求出2x﹣
,再由ω>0即可求出ω的取值范围;(2)由f(x)的最小正周期为π求出ω的值,代入f(x)的解析式,根据x的范围求出2x﹣ ![]() 范围,根据正弦函数的图像与性质得到f(x)取得最大值时x的值,把求出x的值及f(x)的最大值为2代入f(x)解析式,即可求出k的值.
范围,根据正弦函数的图像与性质得到f(x)取得最大值时x的值,把求出x的值及f(x)的最大值为2代入f(x)解析式,即可求出k的值.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设 ![]() ,g(x)=ax+5﹣2a(a>0).
,g(x)=ax+5﹣2a(a>0).
(1)求f(x)在x∈[0,1]上的值域;
(2)若对于任意x1∈[0,1],总存在x0∈[0,1],使得g(x0)=f(x1)成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() :
: ![]() (
(![]() 为参数,
为参数, ![]() ),在以坐标原点为极点,
),在以坐标原点为极点, ![]() 轴的非负半轴为极轴的极坐标系中,曲线
轴的非负半轴为极轴的极坐标系中,曲线![]() :
: ![]() .
.
(1)试将曲线![]() 与
与![]() 化为直角坐标系
化为直角坐标系![]() 中的普通方程,并指出两曲线有公共点时
中的普通方程,并指出两曲线有公共点时![]() 的取值范围;
的取值范围;
(2)当![]() 时,两曲线相交于
时,两曲线相交于![]() ,
, ![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,A1C1⊥B1D1 , E,F分别是AB,BC的中点. 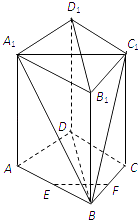
(1)求证:EF∥平面A1BC1;
(2)求证:平面D1DBB1⊥平面A1BC1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的几何体![]() 中,底面
中,底面![]() 为菱形,
为菱形, ![]() ,
, ![]() ,
, ![]() 与
与![]() 相交于
相交于![]() 点,四边形
点,四边形![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 底面
底面![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(0,1)、B(0,2)、C(4t,2t2﹣1)(t∈R),⊙M是以AC为直径的圆,再以M为圆心、BM为半径作圆交x轴交于D、E两点.
(Ⅰ)若△CDE的面积为14,求此时⊙M的方程;
(Ⅱ)试问:是否存在一条平行于x轴的定直线与⊙M相切?若存在,求出此直线的方程;若不存在,请说明理由;
(Ⅲ)求 ![]() 的最大值,并求此时∠DBE的大小.
的最大值,并求此时∠DBE的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个正三角形等分成4个全等的小正三角形,将中间的一个正三角形挖掉(如图1),再将剩余的每个正三角形分成4个全等的小正三角形,并将中间的一个正三角形挖掉,得图2,如此继续下去… 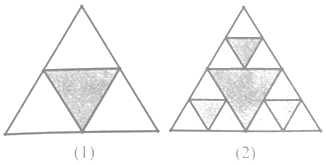
(1)图3共挖掉多少个正三角形?
(2)设原正三角形边长为a,第n个图形共挖掉多少个正三角形?这些正三角形面积和为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三角形ABC的顶点坐标为A(﹣1,5)、B(﹣2,﹣1)、C(4,3).
(1)求AB边上的高线所在的直线方程;
(2)求三角形ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com