
【题目】如图所示,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=![]() ,则下列结论中错误的是
,则下列结论中错误的是

A.AC⊥BE B.EF∥平面ABCD
C.三棱锥A-BEF的体积为定值 D.异面直线AE,BF所成的角为定值
【答案】D
【解析】连接BD,∵AC⊥平面BB1D1D,又BE平面BB1D1D,∴AC⊥BE,故A正确.
∵B1D1∥平面ABCD,又E、F在直线D1B1上运动,∴EF∥平面ABCD,故B正确.
C中由于点B到直线B1D1的距离不变,故△BEF的面积为定值,又点A到平面BEF的距离为![]() ,故VA-BEF为定值.故C正确.
,故VA-BEF为定值.故C正确.
当点E在D1处,点F为D1B1的中点时,建立空间直角坐标系,如图所示,可得A(1,1,0),B(0,1,0),E(1,0,1),F![]() ,∴
,∴![]() =(0,-1,1),
=(0,-1,1),![]() =
=![]() ,∴cos〈
,∴cos〈![]() ,
,![]() 〉=
〉=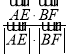 =
=![]() ,此时异面直线AE与BF所成的角为30°.
,此时异面直线AE与BF所成的角为30°.
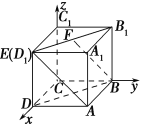
当点E为D1B1的中点,点F在B1处时,此时E![]() ,F(0,1,1),∴
,F(0,1,1),∴![]() =
=![]() ,
,![]() =(0,0,1),∴cos〈
=(0,0,1),∴cos〈![]() ,
,![]() 〉=
〉= =
=![]() =
=![]() ≠
≠![]() ,故选项D不正确.故选D.
,故选项D不正确.故选D.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求![]() 的值;
的值;
(2)若函数![]() 在区间
在区间![]() 是单调递增函数,求实数
是单调递增函数,求实数![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 内有两个实数根
内有两个实数根![]() ,记
,记![]() ,求实数
,求实数![]() 的取值范围 .
的取值范围 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据用户对产品的满意度评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频数分布表。

A地区用户满意度评分的频率分布直方图

B地区用户满意度评分的频数分布表
(Ⅰ)在答题卡上作出B地区用户满意度评分的频率分布直方图,并通过直方图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,给出结论即可);
(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
估计哪个地区的满意度等级为不满意的概率大?说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱台ABCDEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.
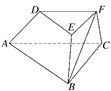
(1)求证:BF⊥平面ACFD;
(2)求二面角B-AD-F的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C经过P(4,-2),Q(-1,3)两点,且圆心在x轴上。
(1)求直线PQ的方程;
(2)圆C的方程;
(3)若直线l∥PQ,且l与圆C交于点A,B,且以线段AB为直径的圆经过坐标原点,求直线l的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司近年来科研费用支出![]() 万元与公司所获利润
万元与公司所获利润![]() 万元之间有如表的统计
万元之间有如表的统计
![]()
数据:参考公式:用最小二乘法求出![]() 关于
关于![]() 的线性回归方程为:
的线性回归方程为: ![]() ,
,
其中: 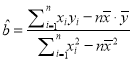 ,
, ![]() ,参考数值:
,参考数值: ![]() 。
。
(Ⅰ)求出![]() ;
;
(Ⅱ)根据上表提供的数据可知公司所获利润![]() 万元与科研费用支出
万元与科研费用支出![]() 万元线性相关,请用最小二乘法求出
万元线性相关,请用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅲ)试根据(Ⅱ)求出的线性回归方程,预测该公司科研费用支出为10万元时公司所获得的利润。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com