
分析 (Ⅰ)利用曲线C上任意一点M满足|MF1|+|MF2|=4,其中F1($0,-\sqrt{3})$,F2($0,\sqrt{3})$,求出几何量,即可得到椭圆的方程;
(Ⅱ)直线方程代入椭圆方程,利用韦达定理,及x1x2+y1y2=0,即可求得结论.
解答 解:(Ⅰ)设椭圆的焦半距为c,则由题设,得a=2,c=$\sqrt{3}$,
所以b2=a2-c2=4-3=1,
故所求椭圆C的方程为$\frac{y^2}{4}+{x^2}=1$.
(Ⅱ)存在实数k使得以线段AB为直径的圆恰好经过坐标原点O.
理由如下:
设点A(x1,y1),B(x2,y2),
将直线l的方程$y=kx+\sqrt{3}$代入$\frac{y^2}{4}+{x^2}=1$,
并整理,得$({k^2}+4){x^2}+2\sqrt{3}kx-1=0$.(*)
则${x_1}+{x_2}=-\frac{{2\sqrt{3}k}}{{{k^2}+4}}$,${x_1}{x_2}=-\frac{1}{{{k^2}+4}}$.
因为以线段AB为直径的圆恰好经过坐标原点O,
所以$\overrightarrow{OA}•\overrightarrow{OB}=0$,即x1x2+y1y2=0.
又${y_1}{y_2}={k^2}{x_1}{x_2}+\sqrt{3}k({x_1}+{x_2})+3$,
于是$-\frac{{1+{k^2}}}{{{k^2}+4}}-\frac{{6{k^2}}}{{{k^2}+4}}+3=0$,解得$k=±\frac{{\sqrt{11}}}{2}$,
经检验知:此时(*)式的△>0,符合题意.
所以当$k=±\frac{{\sqrt{11}}}{2}$时,以线段AB为直径的圆恰好经过坐标原点O.
点评 本题考查椭圆的标准方程及其几何性质、直线与椭圆的位置关系,考查韦达定理的运用,属于中档题.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:选择题
| A. | 0.75 | B. | 0.25 | C. | 0.8 | D. | 0.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,1] | B. | [-1,2] | C. | [-1,2) | D. | (-∞,-1]∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{3}$,1) | B. | ($\frac{1}{3}$,1) | C. | [$\frac{2}{3}$,1) | D. | ($\frac{2}{3}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
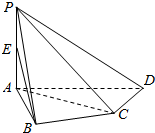 在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PA上的一点.
在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PA上的一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com