练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．长方体ABCD-A1B1C1D1中，E、F分别为线段AA1、B1C上的点，若AB=6，BC=5．AA1=3．则三棱锥D1-EDF的体积为（　　）
    A．$\frac{15}{2}$B．15
    C．30D．随点E、F的改变而改变的值

    分析 因为B1C∥平面EDD1，所以三棱锥D1-EDF的体积等于三棱锥F-EDD1，的体积，棱锥的高为长方体的棱长CD，底面EDD1，是以3为底5为高的三角形，利用棱锥的体积公式可求．

    解答 解：∵B1C∥平面EDD1，
    ∴三棱锥D1-EDF的体积等于三棱锥F-EDD1的体积，而三棱锥F-EDD1，底面EDD1，是以3为底5为高的三角形，三棱锥F-EDD1的高为6，
    ∴V=$\frac{1}{3}×\frac{1}{2}×3×5×6$=15
    故选B．

    点评 本题考查了棱锥的体积，关键是明确三棱锥D1-EDF的体积等于三棱锥F-EDD1的体积，进一步明确其底面面积和高，利用体积公式解答．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    4．已知cosx+cosy=$\frac{\sqrt{2}}{2}$，求sinx+siny的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知四边形ABCD是直角梯形，其中A（0，-1），B（0，2），C（2，0），求D点坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．△ABC中，点M在AC上，且$\overrightarrow{AC}$=3$\overrightarrow{MC}$，点N是BC的中点，若$\overrightarrow{MB}$=（4，3），$\overrightarrow{MN}$=（1，5），则$\overrightarrow{AC}$=（-6，21）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

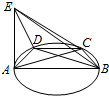    9．已知三棱锥E-ABD各个面均为直角三角形，且Rt△ADE的直角顶点为A，其中AE=AB，∠ABD=$\frac{π}{6}$，以AB为直径在平面ABD内画圆，且经过点D，任取圆上一点C（不与A，B两点重合）．
    （1）求证：△BCE为直径三角形；
    （2）若四边形ABCE为一个等腰梯形，且BC=1，求几何体C-BDE的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．要将一段圆木锯成方木，已知圆木横截面的直径等于d cm，问方木横截面的长与宽为多少时，所得横截面积最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．若三点A（0，a，2b），B（2，3，4），C（3，4，5）共线，则下列等式成立的是（　　）
    A．2a=bB．a+b=2C．2a-b=3D．a-2b=1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．若非零向量$\overrightarrow{a}$，$\overrightarrow{b}$，满足$\overrightarrow{a}$•$\overrightarrow{b}$=0，且|$\overrightarrow{a}$-$\overrightarrow{b}$|=2|$\overrightarrow{a}$|，则向量$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{b}$的夹角为（　　）
    A．$\frac{π}{6}$B．$\frac{π}{3}$C．$\frac{2π}{3}$D．$\frac{5π}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．六本不同的书分给甲、乙、丙三人，每人两本有多少种不同的分法？

    查看答案和解析>>

    同步练习册答案