
ĄūĖâÄŋĄŋËæŨÅļßŋžÖÆķČĩÄļÄļïĢŽÄģĘĄžī―ŦĘĩĘĐĄ°ÓïĘýÍâ+3ĄąÐÂļßŋžĩÄ·―°ļĢŽ2019ÄęĮïžūČëŅ§ĩÄļßŌŧÐÂÉú―ŦÃæÁŲīÓÎïĀíĢĻÎïĢĐĄĒŧŊŅ§ĢĻŧŊĢĐĄĒÉúÎïĢĻÉúĢĐĄĒÕþÖÎĢĻÕþĢĐĄĒĀúĘ·ĢĻĀúĢĐĄĒĩØĀíĢĻĩØĢĐÁųŋÆÖÐČÎŅĄČýŋÆĢĻđē20ÖÖŅĄ·ĻĢĐŨũΊŨÔžš―ŦĀīļßŋžĄ°ÓïĘýÍâ+3ĄąÐÂļßŋž·―°ļÖÐĩÄĄ°3ĄąÄģĘÐΊÁËËģĀûĩØÓ―ÓÐÂļßŋžļÄļïĢŽÔÚÄģļßÖÐ200ÃûŅ§ÉúÖÐ―øÐÐÁËĄ°Ņ§ÉúÄĢÄâŅĄŋÆĘýūÝĄąĩũēéĢŽÃŋļöŅ§ÉúÖŧÄÜīÓąíļņÖÐĩÄ20ÖÖŋÎģĖŨéšÏÖÐŅĄÔņŌŧÖÖŅ§Ï°ÄĢÄâŅĄŋÎĘýūÝÍģžÆČįÏÂąíĢš
ÐōšÅ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
ŨéšÏŅ§ŋÆ | ÎïŧŊÉú | ÎïŧŊÕþ | ÎïŧŊĀú | ÎïŧŊĩØ | ÎïÉúÕþ | ÎïÉúĀú | ÎïÉúĩØ | ÎïÕþĀú | ÎïÕþĩØ | ÎïĀúĩØ |
ČËĘý | 20ČË | 5ČË | 10ČË | 10ČË | 5ČË | 15ČË | 10ČË | 5ČË | 0ČË | 5ČË |
11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | šÏžÆ |
ŧŊÉúÕþ | ŧŊÉúĀú | ŧŊÉúĩØ | ŧŊÕþĀú | ŧŊÕþĩØ | ŧŊĀúĩØ | ÉúÕþĀú | ÉúÕþĩØ | ÉúĀúĩØ | ÕþĀúĩØ | |
5ČË | Ą | Ą | Ą | Ą | Ą | 10ČË | 5ČË | Ą | 25ČË | 200ČË |
ΊÁË―âŅ§ÉúģÉžĻÓëŅ§ÉúÄĢÄâŅĄŋÎĮéŋöÖŪÎĘĩÄđØÏĩĢŽÓ÷ÖēãģéŅųĩÄ·―·ĻīÓÕâ200ÃûŅ§ÉúÖÐģéČĄ40ČËĩÄŅųąū―øÐзÖÎö
(l)ŅųąūÖÐŅĄÔņŨéšÏ20šÅĄ°ÕþĀúĩØĄąĩÄÓÐķāÉŲČËĢŋČôŌÔŅųąūÆĩÂĘŨũΊļÅÂĘĢŽĮóļÃļßÖÐŅ§ÉúēŧŅĄÎïĀíŅ§ŋÆĩÄļÅÂĘĢŋ
(Ēō)īÓŅųąūÖÐŅĄÔņŅ§Ï°ÉúÎïĮŌŅ§Ï°ÕþÖÎĩÄŅ§ÉúÖÐËæŧúģéČĄ3ČËĢŽĮóÕâ3ČËÖÐÖÁÉŲÓÐŌŧČËŧđŅ§Ï°ĀúĘ·ĩÄļÅÂĘĢŋ
Ąūīð°ļĄŋ(Ēņ) 5Ģŧ![]() (Ēō)
(Ēō) ![]()
Ąū―âÎöĄŋ
ĢĻĒņĢĐÓÉąíļņĘýūÝŋÉĩÃŅĄÔņŨéšÏ20šÅĄ°ÕþĀúĩØĄąĩÄČËĘýÕžŨÜČËĘýĩÄąČĀýĢŽČŧšóŋÉĮóģö·ÖģÉģéŅųŅųąūÖÐŅĄÔņŨéšÏ20šÅĄ°ÕþĀúĩØĄąĩÄČËĘýĢŽÓÉąíļņĘýūÝŋÉÖŠĢŽŅĄÎïĀíŅ§ŋÆĩÄ°üšŽ1-10šÅŨéšÏĢŽŋÉËãģöŅĄÎïĀíŅ§ŋÆĩÄČËĘýĢŽÓÖŨÜČËĘý200ĢŽŋÉĩÃēŧŅĄÎïĀíŅ§ŋÆĩÄČËĘýĢŽīÓķøŋÉĮóģöŅųąūÖÐēŧŅĄÎïĀíŅ§ŋÆĩÄČËĘýĢŽČŧšóŋÉžÆËãÆäÆĩÂĘĢŧĢĻĒōĢĐÏČÓÉąíļņÖÐĘýūÝĮóģöŅĄÔņŅ§Ï°ÉúÎïĮŌŅ§Ï°ÕþÖÎĩÄČËĘýšÍŧđŅ§Ï°ĀúĘ·ĩÄČËĘýĢŽīÓķøĮóģöŅųąūÖÐŅĄÔņŅ§Ï°ÉúÎïĮŌŅ§Ï°ÕþÖÎĩÄČËĘýšÍŧđŅ§Ï°ĀúĘ·ĩÄČËĘýĢŽČŧšóÓÃÃķūŲ·ĻĢŽ―ŦŋÉÄÜĩÄĮéŋöŌŧŌŧÁÐģöĀīĢŽÕŌģöÆäÖзûšÏĖâŌâĩÄĮéŋöĘýĢŽÓÉđÅĩäļÅÐÍđŦĘ―ĮóģöļÅÂĘ.
―âĢšĢĻĒņĢĐÓÉ·ÖēãģéŅųŋÉĩÃĢŽŅųąūÖÐŅĄÔņŨéšÏ20šÅĄ°ÕþĀúĩØĄąĩÄÓÐ![]() ČË
ČË
ÓÉąíļņĘýūÝŋÉÖŠĢŽŅĄÎïĀíŅ§ŋÆĩÄ°üšŽ1-10šÅŨéšÏĢŽ
đē![]() ČË
ČË
ÔōēŧŅĄÎïĀíŅ§ŋÆÓÐ![]() ČË
ČË
ËųŌÔŅųąūÖÐēŧŅĄÎïĀíŅ§ŋÆÓÐ![]() ČË
ČË
ÉčĘžþAąíĘūĄ°ļÃļßÖÐŅ§ÉúēŧŅĄÎïĀíŅ§ŋÆĄąĢŽ ŌÔŅųąūÆĩÂĘŨũΊļÅÂĘ
Ôō![]()
ĢĻĒōĢĐÓÉąíļņĘýūÝŋÉÖŠĢŽŅĄÔņŅ§Ï°ÉúÎïĮŌŅ§Ï°ÕþÖÎĩÄŨéšÏÓÐ2šÅĢŽ11šÅĢŽ17šÅĢŽ18šÅĢŽđēÓÐ![]() ČËĢŽÆäÖÐŧđŅ§Ï°ĀúĘ·ĩÄŨéšÏÖŧÓÐ17šÅĢŽđē10ČË
ČËĢŽÆäÖÐŧđŅ§Ï°ĀúĘ·ĩÄŨéšÏÖŧÓÐ17šÅĢŽđē10ČË
ËųŌÔŅųąūÖÐŅĄÔņŅ§Ï°ÉúÎïĮŌŅ§Ï°ÕþÖÎĩÄŅ§ÉúđēÓÐ![]() ČËĢŽ
ČËĢŽ
ÆäÖÐŧđŅ§Ï°ĀúĘ·ĩÄÓÐ![]() ČËĢŽ
ČËĢŽ
ÉčžČŅ§Ï°ÉúÎïšÍÕþÖÎŧđŅ§Ï°ĀúĘ·ĩÄ2ČËΊ![]() ĢŽÆäËû3ČËΊ
ĢŽÆäËû3ČËΊ![]() ĢŽ
ĢŽ
ÔōīÓÖÐČÎŅĄ3ČËĩÄŧųąūĘžþÓÐĢš![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() đē10ÖÖĢŽ
đē10ÖÖĢŽ
ÆäÖзûšÏĖâŌâĩÄŧųąūĘžþđēÓÐ9ÖÖ.
ÓÉđÅĩäļÅÐÍŋÉĩÃĢŽÕâ3ČËÖÐÖÁÉŲÓÐŌŧČËŧđŅ§Ï°ĀúĘ·ĩÄļÅÂĘΊ![]()



| Äęžķ | ļßÖÐŋÎģĖ | Äęžķ | ģõÖÐŋÎģĖ |
| ļßŌŧ | ļßŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõŌŧ | ģõŌŧÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßķþ | ļßķþÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõķþ | ģõķþÃâ·ŅŋÎģĖÍÆžöĢĄ |
| ļßČý | ļßČýÃâ·ŅŋÎģĖÍÆžöĢĄ | ģõČý | ģõČýÃâ·ŅŋÎģĖÍÆžöĢĄ |
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋÔÚĀâģĪΊaĩÄÕý·―ĖåABCD-A1B1C1D1ÖÐĢŽEĘĮĀâDD1ĩÄÖÐĩãĢš
(1)ĮóĩãDĩ―Æ―ÃæA1BEĩÄūāĀëĢŧ
(2)ÔÚĀâ![]() ÉÏĘĮ·ņīæÔÚŌŧĩãFĢŽĘđĩÃB1FĄÎÆ―ÃæA1BEĢŽČôīæÔÚĢŽÖļÃũĩãFĩÄÎŧÖÃĢŧČôēŧīæÔÚĢŽĮëËĩÃũĀíÓÉĄĢ
ÉÏĘĮ·ņīæÔÚŌŧĩãFĢŽĘđĩÃB1FĄÎÆ―ÃæA1BEĢŽČôīæÔÚĢŽÖļÃũĩãFĩÄÎŧÖÃĢŧČôēŧīæÔÚĢŽĮëËĩÃũĀíÓÉĄĢ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠ![]()
ĢĻĒņĢĐÁÐąíĮó![]() ÔÚ
ÔÚ![]() ĩÄËųÓОŦÖĩĢŧ
ĩÄËųÓОŦÖĩĢŧ
ĢĻĒōĢĐĩą![]() ĘąĢŽ
ĘąĢŽ
ĢĻiĢĐĮóÖĪĢš![]() Ģŧ
Ģŧ
ĢĻiiĢĐČô![]() šãģÉÁĒĢŽĮó
šãģÉÁĒĢŽĮó![]() ĩÄČĄÖĩ·ķΧ
ĩÄČĄÖĩ·ķΧ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠšŊĘýfĢĻxĢĐ=aexÍžÏóÔÚx=0īĶĩÄĮÐÏßÓëšŊĘýgĢĻxĢĐ=lnxÍžÏóÔÚx=1īĶĩÄĮÐÏßŧĨÏāÆ―ÐÐĢŪ
ĢĻĒņĢĐĮóaĩÄÖĩĢŧ
ĢĻĒōĢĐÉčÖąÏßx=tĢĻtĢū0ĢĐ·ÖąðÓëĮúÏßy=fĢĻxĢĐšÍy=gĢĻxĢĐ―ŧÓÚPĢŽQÁ―ĩãĢŽĮóÖĪĢš|PQ|Ģū2ĢŪ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋÉčÅŨÎïÏßCĢšy2Ģ―4xĩÄ―đĩãΊFĢŽđýFĩÄÖąÏßlÓëC―ŧÓÚAĢŽBÁ―ĩãĢŽĩãMĩÄŨøąęΊĢĻĐ1ĢŽ0ĢĐ.
ĢĻ1ĢĐĩąlÓëxÖáīđֹʹĢŽĮóĄũABMĩÄÍâ―ÓÔē·―ģĖĢŧ
ĢĻ2ĢĐžĮĄũAMFĩÄÃæŧýΊS1ĢŽĄũBMFĩÄÃæŧýΊS2ĢŽĩąS1Ģ―4S2ĘąĢŽĮóÖąÏßlĩÄ·―ģĖ.
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŌŅÖŠËŦĮúÏß![]() Ģ―1(aĢū0ĢŽbĢū0)ĩÄŨóĄĒÓŌ―đĩã·ÖąðΊF1ĢŽF2ĢŽĩãOΊËŦĮúÏßĩÄÖÐÐÄĢŽĩãPÔÚËŦĮúÏßÓŌÖ§ÉÏĢŽĄũPF1F2ÄÚĮÐÔēĩÄÔēÐÄΊQĢŽÔēQÓëxÖáÏāĮÐÓÚĩãAĢŽđýF2ŨũÖąÏßPQĩÄīđÏßĢŽīđŨãΊBĢŽÔōÏÂÁÐ―áÂÛģÉÁĒĩÄĘĮ( )
Ģ―1(aĢū0ĢŽbĢū0)ĩÄŨóĄĒÓŌ―đĩã·ÖąðΊF1ĢŽF2ĢŽĩãOΊËŦĮúÏßĩÄÖÐÐÄĢŽĩãPÔÚËŦĮúÏßÓŌÖ§ÉÏĢŽĄũPF1F2ÄÚĮÐÔēĩÄÔēÐÄΊQĢŽÔēQÓëxÖáÏāĮÐÓÚĩãAĢŽđýF2ŨũÖąÏßPQĩÄīđÏßĢŽīđŨãΊBĢŽÔōÏÂÁÐ―áÂÛģÉÁĒĩÄĘĮ( )
A. |OA|Ģū|OB|B. |OA|Ģž|OB|
C. |OA|Ģ―|OB|D. |OA|Óë|OB|īóÐĄđØÏĩēŧČ·ķĻ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋ![]() ÄęĢŽÔÚĮėŨĢÖÐŧŠČËÃņđēšÍđúģÉÁĒ
ÄęĢŽÔÚĮėŨĢÖÐŧŠČËÃņđēšÍđúģÉÁĒ![]() ÖÜÄęÖŪžĘĢŽÓÖÓĀīÁËŌÔĄ°īīūüČËČŲŌŦĢŽÖþĘĀ―įšÍÆ―ĄąÎŠŨÚÖžĩÄĩÚÆß―ėĘĀ―įūüČËÔËķŊŧáĢŪūÝÏĪĢŽÕâīÎūüÔËŧá―ŦÓÚ
ÖÜÄęÖŪžĘĢŽÓÖÓĀīÁËŌÔĄ°īīūüČËČŲŌŦĢŽÖþĘĀ―įšÍÆ―ĄąÎŠŨÚÖžĩÄĩÚÆß―ėĘĀ―įūüČËÔËķŊŧáĢŪūÝÏĪĢŽÕâīÎūüÔËŧá―ŦÓÚ![]() Äę
Äę![]() ÔÂ
ÔÂ![]() ČÕÖÁ
ČÕÖÁ![]() ČÕÔÚÃĀĀöĩÄ―ģĮÎäššūŲÐÐĢŽ―ėĘą―ŦÓÐĀīŨÔČŦĘĀ―į
ČÕÔÚÃĀĀöĩÄ―ģĮÎäššūŲÐÐĢŽ―ėĘą―ŦÓÐĀīŨÔČŦĘĀ―į![]() ķāļöđúžŌšÍĩØĮøĩÄ―üÍōÃûūüČËÔËķŊÔąēÎČüĢŪÏāķÔÓÚ°ÂÔËŧáĄĒŅĮÔËŧáĩČīóÐÍŨÛšÏČüĘÂĢŽūüÔËŧáŧōÐíķÔšÜķāČËĀīËĩŧđšÜÄ°ÉúĢŪΊīËĢŽÎäššÄģļßÐĢΊÁËÔÚŅ§ÉúÖÐļüđã·šĩÄÍÆ―éÆÕž°ūüÔËŧáÏāđØÖŠĘķÄÚČÝĢŽĖØÔÚÍøÂįÉÏŨéÖŊÁËŌŧīÎĄ°ÎŌËųÖŠÏþĩÄÎäššūüÔËŧ᥹֊ĘķÎĘīðąČČüĢŽÎŠąãÓÚķÔīðūí―øÐÐķÔąČŅÐūŋĢŽŨéÎŊŧáģéČĄÁË
ķāļöđúžŌšÍĩØĮøĩÄ―üÍōÃûūüČËÔËķŊÔąēÎČüĢŪÏāķÔÓÚ°ÂÔËŧáĄĒŅĮÔËŧáĩČīóÐÍŨÛšÏČüĘÂĢŽūüÔËŧáŧōÐíķÔšÜķāČËĀīËĩŧđšÜÄ°ÉúĢŪΊīËĢŽÎäššÄģļßÐĢΊÁËÔÚŅ§ÉúÖÐļüđã·šĩÄÍÆ―éÆÕž°ūüÔËŧáÏāđØÖŠĘķÄÚČÝĢŽĖØÔÚÍøÂįÉÏŨéÖŊÁËŌŧīÎĄ°ÎŌËųÖŠÏþĩÄÎäššūüÔËŧ᥹֊ĘķÎĘīðąČČüĢŽÎŠąãÓÚķÔīðūí―øÐÐķÔąČŅÐūŋĢŽŨéÎŊŧáģéČĄÁË![]() ÃûÄÐÉúšÍ
ÃûÄÐÉúšÍ![]() ÃûÅŪÉúĩÄīðūíĢŽËûÃĮĩÄŋžĘÔģÉžĻÆĩÂĘ·ÖēžÖą·―ÍžČįÏÂĢš
ÃûÅŪÉúĩÄīðūíĢŽËûÃĮĩÄŋžĘÔģÉžĻÆĩÂĘ·ÖēžÖą·―ÍžČįÏÂĢš
ĢĻŨĒĢšÎĘūíÂú·ÖΊ![]() ·ÖĢŽģÉžĻ
·ÖĢŽģÉžĻ![]() ĩÄĘÔūíΊĄ°ÓÅÐãĄąĩČžķĢĐ
ĩÄĘÔūíΊĄ°ÓÅÐãĄąĩČžķĢĐ
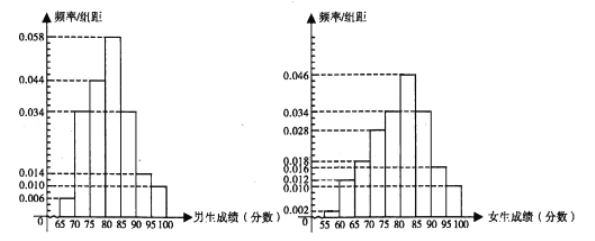
(1)īÓÏÖÓÐ![]() ÃûÄÐÉúšÍ
ÃûÄÐÉúšÍ![]() ÃûÅŪÉúīðūíÖÐļũČĄŌŧ·ÝĢŽ·ÖąðĮóīðūíģÉžĻΊĄ°ÓÅÐãĄąĩČžķĩÄļÅÂĘĢŧ
ÃûÅŪÉúīðūíÖÐļũČĄŌŧ·ÝĢŽ·ÖąðĮóīðūíģÉžĻΊĄ°ÓÅÐãĄąĩČžķĩÄļÅÂĘĢŧ
(2)ĮóÁÐÁŠąíÖÐ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĩÄÖĩĢŽēĒļųūÝÁÐÁŠąíŧØīðĢšÄÜ·ņÔÚ·ļīíÎóĩÄļÅÂĘēŧģŽđý
ĩÄÖĩĢŽēĒļųūÝÁÐÁŠąíŧØīðĢšÄÜ·ņÔÚ·ļīíÎóĩÄļÅÂĘēŧģŽđý![]() ĩÄĮ°ĖáÏÂČÏΊĄ°īðūíģÉžĻΊÓÅÐãĩČžķÓëÐÔąðÓÐđØĄąĢŋ
ĩÄĮ°ĖáÏÂČÏΊĄ°īðūíģÉžĻΊÓÅÐãĩČžķÓëÐÔąðÓÐđØĄąĢŋ
ÄÐ | ÅŪ | ŨÜžÆ | |
ÓÅÐã |
|
|
|
·ĮÓÅÐã |
|
|
|
ŨÜžÆ |
|
|
|
(3)ļųūÝÄÐĄĒÅŪÉúģÉžĻÆĩÂĘ·ÖēžÖą·―ÍžĢŽķÔËûÃĮĩÄģÉžĻĩÄÓÅÁÓ―øÐÐąČ―ÏĢŪ
ļ―ĢšēÎŋžđŦĘ―Ģš![]() ĢŽÆäÖÐ
ĢŽÆäÖÐ![]() .
.
|
|
|
|
|
|
|
|
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋĢĻĮëÐīģöĘ―ŨÓÔÚÐīžÆËã―áđûĢĐÓÐ4ļöēŧÍŽĩÄÐĄĮōĢŽ4ļöēŧÍŽĩÄšÐŨÓĢŽÏÖÔÚŌŠ°ŅĮōČŦēŋ·ÅČëšÐÄÚĢš
ĢĻ1ĢĐđēÓÐķāÉŲÖÖ·―·ĻĢŋ
ĢĻ2ĢĐČôÃŋļöšÐŨÓēŧŋÕĢŽđēÓÐķāÉŲÖÖēŧÍŽĩÄ·―·ĻĢŋ
ĢĻ3ĢĐĮĄÓÐŌŧļöšÐŨÓēŧ·ÅĮōĢŽđēÓÐķāÉŲÖÖ·Å·ĻĢŋ
ēéŋīīð°ļšÍ―âÎö>>
ŋÆÄŋĢšļßÖÐĘýŅ§ ĀīÔīĢš ĖâÐÍĢš
ĄūĖâÄŋĄŋŅĄÐÞ4-5ĢšēŧĩČĘ―ŅĄ―ē
ŌŅÖŠšŊĘý![]() .
.
ĢĻĒņĢĐČô![]() ĢŽ―âēŧĩČĘ―
ĢŽ―âēŧĩČĘ―![]() Ģŧ
Ģŧ
ĢĻĒōĢĐĩą![]() ĘąĢŽšŊĘý
ĘąĢŽšŊĘý![]() ĩÄŨîÐĄÖĩΊ
ĩÄŨîÐĄÖĩΊ![]() ĢŽĮóĘĩĘý
ĢŽĮóĘĩĘý![]() ĩÄÖĩ.
ĩÄÖĩ.
ēéŋīīð°ļšÍ―âÎö>>
°ŲķČÖÂÐÅ - Á·Ï°ēáÁÐąí - ĘÔĖâÁÐąí
šþąąĘĄŧĨÁŠÍøÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻÆ―ĖĻ | ÍøÉÏÓКĶÐÅÏĒūŲąĻŨĻĮø | ĩįÐÅÕĐÆūŲąĻŨĻĮø | ÉæĀúĘ·ÐéÎÞÖũŌåÓКĶÐÅÏĒūŲąĻŨĻĮø | ÉæÆóĮÖČĻūŲąĻŨĻĮø
ÎĨ·ĻšÍēŧÁžÐÅÏĒūŲąĻĩįŧ°Ģš027-86699610 ūŲąĻÓĘÏäĢš58377363@163.com