
 和P,且各株大树是否成活互不影响.已知两种大树各成活1株的概率为
和P,且各株大树是否成活互不影响.已知两种大树各成活1株的概率为 .
.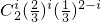 ;
;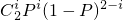 .
.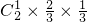 ×
×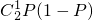 =
= ,即(2P-1)2=0,
,即(2P-1)2=0, …(3分)
…(3分)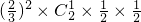 +
+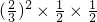 +
+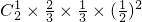 =
=
 .…(6分)
.…(6分)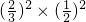 +
+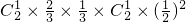 +
+ =
=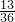 ,
,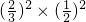 +
+ =
= ,
,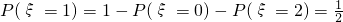
| ξ | 0 | 1 | 2 |
| P | 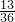 |  |  |
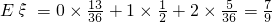 …(12分)
…(12分)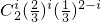 ,设“乙种大树恰有i株成活”为事件Bi(i=0,1,2),则P(Bi)=
,设“乙种大树恰有i株成活”为事件Bi(i=0,1,2),则P(Bi)=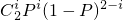 .
.

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 5 |
| 6 |
| 4 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 2 |
| 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分13分,(Ⅰ)问7分,(Ⅱ)问6分)
某单位为绿化环境,移栽了甲、乙两种大树各2株。设甲、乙两种大树移栽的成活率分别为![]() 和
和![]() ,且各株大树是否成活互不影响。求移栽的4株大树中:
,且各株大树是否成活互不影响。求移栽的4株大树中:
(Ⅰ)至少有1株成活的概率;
(Ⅱ)两种大树各成活1株的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分13分,(Ⅰ)问7分,(Ⅱ)问6分)
某单位为绿化环境,移栽了甲、乙两种大树各2株。设甲、乙两种大树移栽的成活率分别为![]() 和
和![]() ,且各株大树是否成活互不影响。求移栽的4株大树中:
,且各株大树是否成活互不影响。求移栽的4株大树中:
(Ⅰ)至少有1株成活的概率;
(Ⅱ)两种大树各成活1株的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com