
如图,椭圆Q:![]() =1(a>b>0)的右焦点为F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P为线段AB的中点.
=1(a>b>0)的右焦点为F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P为线段AB的中点.
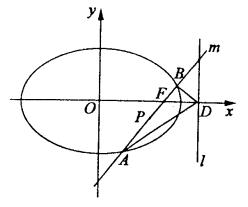
(1)求点P的轨迹H的方程;
(2)若在Q的方程中,令a2=1+cosθ+sinθ,b2=sinθ(0<θ≤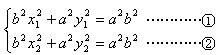 ).
).
设轨迹H的最高点和最低点分别为M和N.当θ为何值时,△MNF为—个正三角形?
如图,

(1)设椭圆Q:![]() =1上的点A(x1,y1)、B(x2,y2),又设P点坐标为P(x,y),则
=1上的点A(x1,y1)、B(x2,y2),又设P点坐标为P(x,y),则
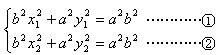
由①-②得
b2(x1-x2)2x+a2(y1-y2)2y=0.
1°当AB不垂直x轴时,x1≠x2
得到![]() 化简得:
化简得:
b2x2+a2y2-b2cx=0……(*)
2°当AB垂直于x轴时,点P即为点F,满足方程(*)
所以点P的轨迹H的方程为:b2x2+a2y2-b2cx=0
(2)因为轨迹H的方程可化为:
∴M(![]() ),N(
),N(![]() ),F(c,0),使△MNF为一个正三角形时,
),F(c,0),使△MNF为一个正三角形时,
则 ,即a2=3b2.
,即a2=3b2.
由于a2=1+cosθ+sinθ,b2=sinθ(0<θ≤![]() ),
),
则1+cosθ+sinθ=3sinθ,得θ=2arctan![]() (或表示为θ=arctan
(或表示为θ=arctan![]() ).
).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
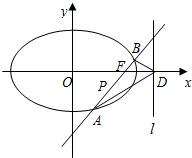 如图,椭圆Q:
如图,椭圆Q:| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,椭圆Q:
如图,椭圆Q:| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
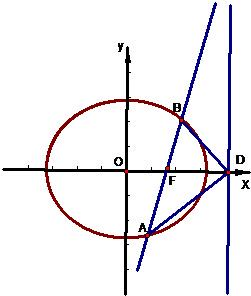
(06年江西卷理)(12分)
如图,椭圆Q:![]() (a>b>0)的右焦点F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P是线段AB的中点
(a>b>0)的右焦点F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P是线段AB的中点
(1)求点P的轨迹H的方程
(2)在Q的方程中,令a2=1+cosq+sinq,b2=sinq(0<q£![]() ),确定q的值,使原点距椭圆的右准线l最远,此时,设l与x轴交点为D,当直线m绕点F转动到什么位置时,三角形ABD的面积最大?
),确定q的值,使原点距椭圆的右准线l最远,此时,设l与x轴交点为D,当直线m绕点F转动到什么位置时,三角形ABD的面积最大?

查看答案和解析>>
科目:高中数学 来源: 题型:
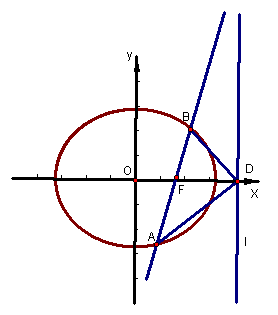
如图,椭圆Q:![]() (a>b>0)的右焦点F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P是线段AB的中点
(a>b>0)的右焦点F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P是线段AB的中点
(1) 求点P的轨迹H的方程
(2) 在Q的方程中,令a2=1+cosq+sinq,b2=sinq(0<q£![]() ),确定q的值,使原点距椭圆的右准线l最远,此时,设l与x轴交点为D,当直线m绕点F转动到什么位置时,三角形ABD的面积最大?
),确定q的值,使原点距椭圆的右准线l最远,此时,设l与x轴交点为D,当直线m绕点F转动到什么位置时,三角形ABD的面积最大?
查看答案和解析>>
科目:高中数学 来源:《第2章 圆锥曲线与方程》2013年单元测试卷(梅河口五中)(解析版) 题型:解答题
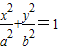 (a>b>0)的右焦点F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P是线段AB的中点.
(a>b>0)的右焦点F(c,0),过点F的一动直线m绕点F转动,并且交椭圆于A、B两点,P是线段AB的中点. ),确定q的值,使原点距椭圆的右准线l最远,此时,设l与x轴交点为D,当直线m绕点F转动到什么位置时,三角形ABD的面积最大?
),确定q的值,使原点距椭圆的右准线l最远,此时,设l与x轴交点为D,当直线m绕点F转动到什么位置时,三角形ABD的面积最大?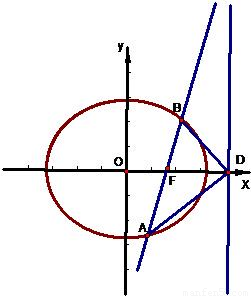
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com