已知集合A={x|x2-7x-18≥0},集合B={x|2x+1>0},集合C={x|m+2<x<2m-3}.
(Ⅰ)设全集U=R,求∁UA∪B;
(Ⅱ)若A∩C=C,求实数m的取值范围.
【答案】
分析:(I)由题设知,应先化简两个集合,再根据补集的定义与并集的定义求出∁
UA∪B;
(II)题目中条件得出“C⊆A”,说明集合C是集合A的子集,由此分C=∅和C≠∅讨论,列端点的不等关系解得实数m的取值范围.
解答:解:(I)由x
2-7x-18≥0得x≤-2,或x≥9,即A=(-∞,-2]∪[9,+∞),
由2x+1>0解得x≥-

,即B=[-

,+∞),
∴∁
UA=(-2,9);
∁
UA∪B=(-2,9);
(II)由A∩C=C得:C⊆A,则
当C=∅时,m+2≥2m-3,⇒m≤5,
当C≠∅时,m+2≥2m-3,⇒m≤5,

或
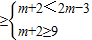
,
解得m≥7,
所以m∈{m|m≤5或m≥7};
点评:本题考查补集与交、并集的求法,属于集合运算中的常规,掌握运算的定义是正确解答的关键.

 ,即B=[-
,即B=[- ,+∞),
,+∞), 或
或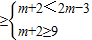 ,
,
