
①a=(2,3,-1),b=(-6,-9,3);
②a=(5,0,2),b=(0,4,0);
③a=(-2,1,4),b=(6,3,3).
(2)设u、v分别是平面α、β的法向量,根据下列条件判断α、β的位置关系:
①u=(1,-1,2),v=(3,2,-![]() );
);
②u=(0,3,0),v=(0,-5,0);
③u=(2,-3,4),v=(4,-2,1).
(3)设u是平面α的法向量,a是直线l的方向向量,根据下列条件判断α和l的位置关系:
①u=(2,2,-1),a=(-3,4,2);
②u=(0,2,-3),a=(0,-8,12);
③u=(4,1,5),a=(2,-1,0).
解:(1)①因为a=(2,3,-1),b=(-6,-9,3),所以a=-![]() b.
b.
所以a∥b.所以l1∥l2.
②因为a=(5,0,2),b=(0,4,0),所以a·b=0.
所以a⊥b.所以l1⊥l2.
③因为a=(-2,1,4),b=(6,3,3),所以a与b不共线,也不垂直,所以l1与l2的位置关系是相交或异面.
(2)①因为u=(1,-1,2),v=(3,2,-![]() ),所以u·v=3-2-1=0.所以u⊥v.所以α⊥β.
),所以u·v=3-2-1=0.所以u⊥v.所以α⊥β.
②因为u=(0,3,0),v=(0,-5,0),
所以u=-![]() v.所以u∥v.所以α∥β.
v.所以u∥v.所以α∥β.
③因为u=(2,-3,4),v=(4,-2,1),
所以u与v既不共线,也不垂直.
所以平面α和β相交(不垂直).
(3)①因为u=(2,2,-1),a=(-3,4,2),所以u·a=-6+8-2=0.所以u⊥a.所以直线l和平面α的位置关系是l![]() α或l∥α.
α或l∥α.
②因为u=(0,2,-3),a=(0,-8,12),所以u=-![]() a.所以u∥a.所以l⊥α.
a.所以u∥a.所以l⊥α.
③因为u=(4,1,5),a=(2,-1,0),所以u和a不共线也不垂直,所以l与α相交(斜交).
绿色通道:
第(1)小题直线方向向量与直线位置关系间的内在联系是:l1∥l2![]() a∥b,l1⊥l2
a∥b,l1⊥l2![]() a⊥b,据此可判断两直线的位置关系;第(2)小题平面法向量与两平面位置关系间的内在联系是:α∥β
a⊥b,据此可判断两直线的位置关系;第(2)小题平面法向量与两平面位置关系间的内在联系是:α∥β![]() u∥v,α⊥β
u∥v,α⊥β![]() u⊥v,据此可判断两平面的位置关系;第(3)小题直线方向向量与平面法向量的关系和直线与平面位置关系之间的内在联系是:l∥α
u⊥v,据此可判断两平面的位置关系;第(3)小题直线方向向量与平面法向量的关系和直线与平面位置关系之间的内在联系是:l∥α![]() a⊥u,l⊥α
a⊥u,l⊥α![]() a∥u.解答上述三类问题的关键:一是要搞清直线方向向量、平面法向量和直线、平面位置关系之间的内在联系,二是要熟练掌握判断两向量共线、垂直等的重要条件.
a∥u.解答上述三类问题的关键:一是要搞清直线方向向量、平面法向量和直线、平面位置关系之间的内在联系,二是要熟练掌握判断两向量共线、垂直等的重要条件.


科目:高中数学 来源: 题型:
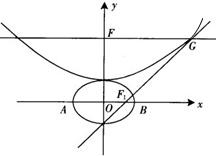 设b>0,椭圆方程为
设b>0,椭圆方程为| x2 |
| 2b2 |
| y2 |
| b2 |
| 1 |
| 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 3 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com