
分析 设x=$\sqrt{3}$m+n,y=$\sqrt{3}$a+b,m,n,a,b∈Q,利用新定义证明即可,设当f(x)=x,x∈Q满足条件,设m,n∈Q,根据新定义验证即可.
解答 解:设x=$\sqrt{3}$m+n,y=$\sqrt{3}$a+b,m,n,a,b∈Q,
∴x+y=$\sqrt{3}$m+n+$\sqrt{3}$a+b=$\sqrt{3}$(m+a)+(n+b),m+a,n+b∈Q,
即f(x+y)=f(x)+f(y),
∴xy=($\sqrt{3}$m+n)($\sqrt{3}$a+b)=3ma+$\sqrt{3}$(mb+an)+bn=$\sqrt{3}$(mb+an)+(bn+3ma),mb,an,bn,3ma∈Q,
∴f(xy)=f(x)•f(y),
∴上述定义下,集合$\left\{{\sqrt{3}m+n\left|{m,n∈Q}\right.}\right\}$ 是封闭的,
当f(x)=x,x∈Q满足条件,
设m,n∈Q,
∴f(m+n)=m+n=f(m)+f(n),
f(mn)=mn=f(m)•f(n),
故答案为:是,f(x)=x,x∈Q
点评 本题考查了新定义的应用,关键是掌握题目所告诉的条件,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 13π | B. | 14π | C. | 15π | D. | 16π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
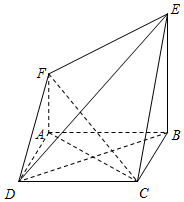 如图,四边形ABCD是边长为2的正方形,平面ABCD⊥平面ABEF,AF∥BE,AB⊥BE,AB=BE=2,AF=1.
如图,四边形ABCD是边长为2的正方形,平面ABCD⊥平面ABEF,AF∥BE,AB⊥BE,AB=BE=2,AF=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
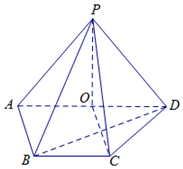 如图,在四棱锥P-ABCD中,O∈AD,AD∥BC,AB⊥AD,AO=AB=BC=1,PO=$\sqrt{2}$,$PC=\sqrt{3}$.
如图,在四棱锥P-ABCD中,O∈AD,AD∥BC,AB⊥AD,AO=AB=BC=1,PO=$\sqrt{2}$,$PC=\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,4,5,6} | B. | {2,3,4,5} | C. | {2,5} | D. | {1,6} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com