
 时,△EFB的面积取得最大值为
时,△EFB的面积取得最大值为 .类比上面的结论,可得,在各棱条相等的体积为V的四面体ABCD中,E是棱AB上的动点,过点E作平面EFG∥平面BCD,分别交AC、AD于点F、G,则四面体EFGB的体积的最大值等于 V.
.类比上面的结论,可得,在各棱条相等的体积为V的四面体ABCD中,E是棱AB上的动点,过点E作平面EFG∥平面BCD,分别交AC、AD于点F、G,则四面体EFGB的体积的最大值等于 V. 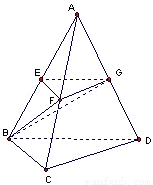 解:根据几何体和平面图形的类比关系,
解:根据几何体和平面图形的类比关系, 时,△EFB的面积取得最大值为
时,△EFB的面积取得最大值为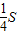 .
. x•x(2-2x)V≤
x•x(2-2x)V≤
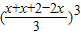 V=
V=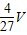 ,最大值等于V四面体EFGB=V四面体AEFG=
,最大值等于V四面体EFGB=V四面体AEFG=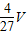 .
.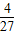 .
.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 4 |
| 4 |
| 27 |
| 4 |
| 27 |
查看答案和解析>>
科目:高中数学 来源:宁德模拟 题型:填空题
| 1 |
| 2 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省苏州市张家港外国语学校高二(上)周日数学试卷5(理科)(解析版) 题型:填空题
 时,△EFB的面积取得最大值为
时,△EFB的面积取得最大值为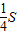 .类比上面的结论,可得,在各棱条相等的体积为V的四面体ABCD中,E是棱AB上的动点,过点E作平面EFG∥平面BCD,分别交AC、AD于点F、G,则四面体EFGB的体积的最大值等于 V.
.类比上面的结论,可得,在各棱条相等的体积为V的四面体ABCD中,E是棱AB上的动点,过点E作平面EFG∥平面BCD,分别交AC、AD于点F、G,则四面体EFGB的体积的最大值等于 V.查看答案和解析>>
科目:高中数学 来源:2012年福建省宁德市高三毕业班质量检查数学试卷(理科)(解析版) 题型:解答题
 时,△EFB的面积取得最大值为
时,△EFB的面积取得最大值为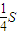 .类比上面的结论,可得,在各棱条相等的体积为V的四面体ABCD中,E是棱AB上的动点,过点E作平面EFG∥平面BCD,分别交AC、AD于点F、G,则四面体EFGB的体积的最大值等于 V.
.类比上面的结论,可得,在各棱条相等的体积为V的四面体ABCD中,E是棱AB上的动点,过点E作平面EFG∥平面BCD,分别交AC、AD于点F、G,则四面体EFGB的体积的最大值等于 V.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com