8.边长为1的菱形ABCD中,∠DAB=60°,−−→CM=−−→MD,−−→ND=2−−→BN,则−−−→AM∙−−→AN=1312.
分析 画出图形,根据条件可得出−−→DM=12−−→AB,−−→DN=23(−−→AB−−−→AD),从而得出−−→AM=−−→AD+12−−→AB,−−→AN=13−−→AD+23−−→AB,这样代入−−→AM∙−−→AN进行数量积的运算即可.
解答 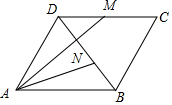 解:如图,
解:如图,
−−→CM=−−→MD;
∴M为DC的中点;
∴−−→DM=12−−→DC=12−−→AB;
−−→ND=2−−→BN;
∴N为线段DB靠近B的三等分点;
∴−−→DN=23−−→DB=23(−−→AB−−−→AD);
∴−−→AM∙−−→AN
=(−−→AD+−−→DM)∙(−−→AD+−−→DN)
=(−−→AD+12−−→AB)∙[−−→AD+23(−−→AB−−−→AD)]
=(−−→AD+12−−→AB)∙(13−−→AD+23−−→AB)
=13−−→AD2+56−−→AB∙−−→AD+13−−→AB2
=13+512+13
=1312.
故答案为:1312.
点评 考查共线向量基本定理,以及向量数乘的几何意义,向量加法和减法的几何意义,向量的数乘运算和数量积运算.

 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案