
【题目】成等差数列的三个正数的和等于15,并且这三个数分别加上2、5、13后成为等比数列{bn}中的b3、b4、b5.
(1)求数列{bn}的通项公式;
(2)数列{bn}的前n项和为Sn,求证:数列![]() 是等比数列.
是等比数列.
【答案】见解析
【解析】
(1)解 设成等差数列的三个正数分别为a-d,a,a+d.
依题意,得a-d+a+a+d=15.
解得a=5.
所以{bn}中的b3,b4,b5依次为7-d,10,18+d.
依题意,有(7-d)(18+d)=100,
解得d=2或d=-13(舍去).
故{bn}的第3项为5,公比为2.
由b3=b1·22,即5=b1·22,
解得b1=![]() .
.
所以bn=b1·qn-1=![]() ·2n-1=5·2n-3,
·2n-1=5·2n-3,
即数列{bn}的通项公式bn=5·2n-3.
(2)证明 由(1)得数列{bn}的前n项和
Sn= =5·2n-2-
=5·2n-2-![]() ,即Sn+
,即Sn+![]() =5·2n-2.
=5·2n-2.
所以S1+![]() =
=![]() ,
,![]() =
=![]() =2.
=2.
因此![]() 是以
是以![]() 为首项,2为公比的等比数列.
为首项,2为公比的等比数列.


科目:高中数学 来源: 题型:
【题目】选修4-4;坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点, ![]() 轴正半轴为极轴的极坐标中,曲线
轴正半轴为极轴的极坐标中,曲线![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程.
的直角坐标方程.
(Ⅱ)求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为(-2,2),函数g(x)=f(x-1)+f(3-2x).
(1)求函数g(x)的定义域;
(2)若f(x)是奇函数,且在定义域上单调递减,求不等式g(x)≤0的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 是半圆
是半圆![]() 的直径,
的直径,![]() ,
,![]() 是将半圆圆周四等分的三个分点.
是将半圆圆周四等分的三个分点.

(1)从![]() 这5个点中任取3个点,求这3个点组成直角三角形的概率;
这5个点中任取3个点,求这3个点组成直角三角形的概率;
(2)在半圆内任取一点![]() ,求
,求![]() 的面积大于
的面积大于![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
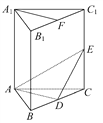
【题目】如图,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥DE,F为B1C1的中点.
求证:(1)平面ADE⊥平面BCC1B1.
(2)直线A1F∥平面ADE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017届江西省南昌市高三第一次模拟考试数学(理)】已知函数![]() (
(![]() ,
,![]() 是自然对数的底数).
是自然对数的底数).
(1)若![]() 是
是![]() 上的单调递增函数,求实数
上的单调递增函数,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,证明:函数
时,证明:函数![]() 有最小值,并求函数
有最小值,并求函数![]() 最小值的取值范围.
最小值的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017届河北省衡水中学高三上学期六调】已知函数![]() ,其中
,其中![]() 均为实数,
均为实数,![]() 为自然对数的底数.
为自然对数的底数.
(1)求函数![]() 的极值;
的极值;
(2)设![]() ,若对任意的
,若对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的左焦点F为圆
的左焦点F为圆![]() 的圆心,且椭圆C上的点到点F的距离最小值为
的圆心,且椭圆C上的点到点F的距离最小值为![]() 。
。
(I)求椭圆C的方程;
(II)已知经过点F的动直线![]() 与椭圆C交于不同的两点A、B,点M坐标为(
与椭圆C交于不同的两点A、B,点M坐标为(![]() ),证明:
),证明: ![]() 为定值。
为定值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017兰州高考模拟】.在多面体ABCDEF中,底面ABCD是梯形,四边形ADEF是正方形,AB∥DC,AB=AD=1,CD=2,AC=EC=![]() 。
。
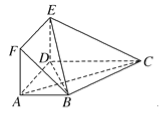
(1)求证:平面EBC⊥平面EBD;
(2)设M为线段EC上一点,且3EM=EC,试问在线段BC上是否存在一点T,使得MT∥平面BDE,若存在,试指出点T的位置;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com