
已知函数 .
.
(1)判断函数 的奇偶性并证明;
的奇偶性并证明;
(2)当 时,求函数
时,求函数 的值域.
的值域.
(1)奇函数,(2)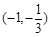 .
.
解析试题分析:(1)判断函数奇偶性,从两个方面入手,一要判断定义域,若定义域不关于原点对称,则函数就为非奇非偶函数,二在函数定义域关于原点对称前提下,判断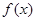 与
与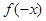 的关系,如只相等,则为偶函数,如只相反,则为奇函数,如既相等又相反,则既为奇函数又为偶函数,如既不相等又不相反,则为非奇非偶函数,本题定义域为R,研究
的关系,如只相等,则为偶函数,如只相反,则为奇函数,如既相等又相反,则既为奇函数又为偶函数,如既不相等又不相反,则为非奇非偶函数,本题定义域为R,研究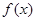 与
与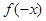 的关系时需将负指数化为对应正指数的倒数,(2)研究函数的值域,一要看函数解析式的结构,本题是可化为
的关系时需将负指数化为对应正指数的倒数,(2)研究函数的值域,一要看函数解析式的结构,本题是可化为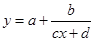 型,二是结合定义域利用函数单调性求值域.
型,二是结合定义域利用函数单调性求值域.
试题解析:(1)∵ ,
,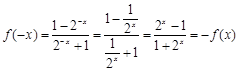 , 4分
, 4分
∴ 是奇函数. 5分
是奇函数. 5分
(2)令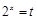 ,则
,则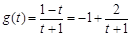 . 7分
. 7分
∵ ,∴
,∴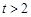 ,∴
,∴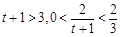 ,∴
,∴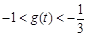 ,
,
所以 的值域是
的值域是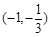 . 10分
. 10分
考点:函数奇偶性,函数值域.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
某医药研究所开发一种新药,在试验药效时发现:如果成人按规定剂量服用,那么服药后每毫升血液中的含药量y(微克)与时间x(小时)之间满足y= 其对应曲线(如图所示)过点
其对应曲线(如图所示)过点 .
. 
(1)试求药量峰值(y的最大值)与达峰时间(y取最大值时对应的x值);
(2)如果每毫升血液中含药量不少于1微克时治疗疾病有效,那么成人按规定剂量服用该药后一次能维持多长的有效时间(精确到0.01小时)?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 (其中
(其中 且
且 ),
), 是
是 的反函数.
的反函数.
(1)已知关于 的方程
的方程 在区间
在区间 上有实数解,求实数
上有实数解,求实数 的取值范围;
的取值范围;
(2)当 时,讨论函数
时,讨论函数 的奇偶性和增减性;
的奇偶性和增减性;
(3)设 ,其中
,其中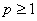 .记
.记 ,数列
,数列 的前
的前 项的和为
项的和为 (
( ),
),
求证: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 (a为常数)在x=1处的切线的斜率为1.
(a为常数)在x=1处的切线的斜率为1.
(1)求实数a的值,并求函数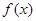 的单调区间,
的单调区间,
(2)若不等式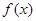 ≥k在区间
≥k在区间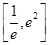 上恒成立,其中e为自然对数的底数,求实数k的取值范围.
上恒成立,其中e为自然对数的底数,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数 的定义域是
的定义域是 ,对于任意的
,对于任意的 ,有
,有 ,且当
,且当 时,
时, .
.
(1)求 的值;
的值;
(2)判断函数的奇偶性;
(3)用函数单调性的定义证明函数 为增函数;
为增函数;
(4)若 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com