
【题目】古希腊人常用小石子在沙滩上摆成各种形状来研究数.比如: 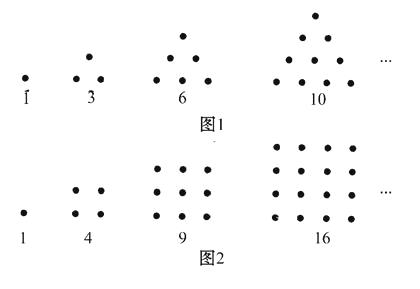
他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16,…,这样的数为正方形数.下列数中既是三角形数又是正方形数的是( )
A.289
B.1024
C.1225
D.1378
科目:高中数学 来源: 题型:
【题目】汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆);
轿车A | 轿车B | 轿车C | |
舒适型 | 100 | 150 | z |
标准型 | 300 | 450 | 600 |
按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(1)求z的值;
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本,将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2.把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() (x>0).
(x>0).
(1)试判断函数f(x)在(0,+∞)上单调性并证明你的结论;
(2)若f(x)> ![]() 恒成立,求整数k的最大值;
恒成立,求整数k的最大值;
(3)求证:(1+1×2)(1+2×3)…[1+n(n+1)]>e2n﹣3 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,E,F分别为PA,BD中点,PA=PD=AD=2.
(Ⅰ)求证:EF∥平面PBC;
(Ⅱ)求二面角E﹣DF﹣A的余弦值;
(Ⅲ)在棱PC上是否存在一点G,使GF⊥平面EDF?若存在,指出点G的位置;若不存在,说明理由.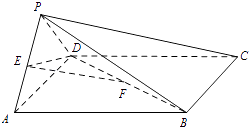
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足:a3=6,a5+a7=24,{an}的前n项和为Sn .
(1)求an及Sn;
(2)令bn= ![]() (n∈N+),求数列{bn}的前n项和Tn .
(n∈N+),求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,椭圆
中,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
, ![]() 也是抛物线
也是抛物线![]() 的焦点,点
的焦点,点![]() 为
为![]() 与
与![]() 在第一象限的交点,且
在第一象限的交点,且![]() .
.
(1)求![]() 的方程;
的方程;
(2)平面上的点![]() 满足
满足![]() ,直线
,直线![]() ,且与
,且与![]() 交于
交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线经过两条直线l1:3x+4y﹣5=0和l2:2x﹣3y+8=0的交点M.
(1)若直线l与直线2x+y+2=0垂直,求直线l的方程;
(2)若直线l′与直线l1关于点(1,﹣1)对称,求直线l′的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com