
【题目】已知圆![]() :
:![]() ,圆
,圆![]() :
:![]() .
.
(Ⅰ)设直线![]() 被圆
被圆![]() 所截得的弦的中点为
所截得的弦的中点为![]() ,判断点
,判断点![]() 与圆
与圆![]() 的位置关系;
的位置关系;
(Ⅱ)设圆![]() 被圆
被圆![]() 截得的一段圆弧(在圆
截得的一段圆弧(在圆![]() 内部,含端点)为
内部,含端点)为![]() ,若直线
,若直线![]() :
:![]() 与圆弧
与圆弧![]() 只有一个公共点,求实数
只有一个公共点,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)点![]() 在圆
在圆![]() 上.(Ⅱ)
上.(Ⅱ)![]() 或
或![]() .
.
【解析】
(Ⅰ)将直线方程代入圆的方程,消去![]() ,得到
,得到![]() ,则
,则![]() ,从而得到
,从而得到![]() 的横坐标为2,再代入直线方程求出
的横坐标为2,再代入直线方程求出![]() 的坐标,即可判断点与圆
的坐标,即可判断点与圆![]() 的位置关系;
的位置关系;
(2)设![]() 和
和![]() 的交点为
的交点为![]() ,
,![]() ,直线
,直线![]() 恒过的定点为
恒过的定点为![]() ,求出两圆的交点坐标,
,求出两圆的交点坐标,
分直线![]() 与圆
与圆![]() 相切时,与直线
相切时,与直线![]() 与圆弧
与圆弧![]() 相交两种情况计算可得.
相交两种情况计算可得.
解:(1)将![]() 代入圆
代入圆![]() 的方程可得
的方程可得![]() .
.
设此方程的两实根分别为![]() ,
,![]() ,则
,则![]() .
.
所以点![]() 的横坐标为2,从而可得
的横坐标为2,从而可得![]() .
.
因为![]() ,所以点
,所以点![]() 在圆
在圆![]() 上.
上.
(Ⅱ)如图,因为直线![]() :
:![]() ,
,![]() 解得
解得![]() ,即直线恒过的定点为
,即直线恒过的定点为![]() .
.
设![]() 和
和![]() 的交点为
的交点为![]() ,
,![]() ,直线
,直线![]() 恒过的定点为
恒过的定点为![]() .
.
由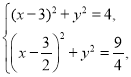 解得
解得![]() ,
,![]() .
.
所以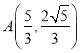 ,
,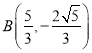 .
.
(ⅰ)当直线![]() 与圆
与圆![]() 相切时.
相切时.
由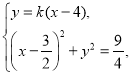 可得
可得![]() .
.
令![]() ,则
,则![]() .
.
此时解得![]() ,切点在圆弧
,切点在圆弧![]() 上,符合题意.
上,符合题意.
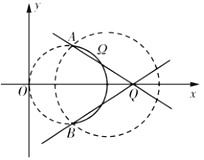
(ⅱ)当直线![]() 与圆弧
与圆弧![]() 相交时,由图可知,要使交点只有一个,则
相交时,由图可知,要使交点只有一个,则![]() 在
在![]() 和
和![]() 之间.
之间.
因为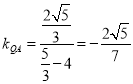 ,
,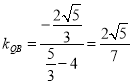 ,
,
所以![]() .
.
综上所述,![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,点D是A1B的中点,点E是B1C1的中点.
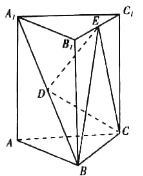
(1)求证:DE∥平面ACC1A1;
(2)若△ABC的面积为![]() ,三棱柱ABC﹣A1B1C1的高为3,求三棱锥D﹣BCE的体积.
,三棱柱ABC﹣A1B1C1的高为3,求三棱锥D﹣BCE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解儿子身高与其父亲身高的关系,随机调查了5对父子的身高,统计数据如下表所示.
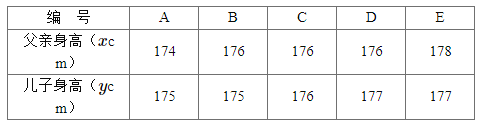
(1)从这五对父子任意选取两对,用编号表示出所有可能取得的结果,并求随机事件M![]() “两对父子中儿子的身高都不低于父亲的身高”发生的概率;
“两对父子中儿子的身高都不低于父亲的身高”发生的概率;
(2)由表中数据,利用“最小二乘法”求![]() 关于
关于![]() 的回归直线的方程.
的回归直线的方程.
参考公式: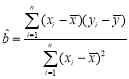 ,
,![]() ;回归直线:
;回归直线:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中“sinA>sinB”是“cosA<cosB”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为![]()
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于![]() 的不等式
的不等式![]() 有且仅有两个正整数解(其中e=2.71828… 为自然对数的底数),则实数
有且仅有两个正整数解(其中e=2.71828… 为自然对数的底数),则实数![]() 的取值范围是( )
的取值范围是( )
A. (![]() ,
,![]() ] B. (
] B. (![]() ,
,![]() ] C. [
] C. [![]() ,
,![]() ) D. [
) D. [![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校有1200名学生,随机抽出300名进行调查研究,调查者设计了一个随机化装置,这是一个装有大小、形状和质量完全相同的10个红球,10个绿球和10个白球的袋子.调查中有两个问题:
问题1:你的阳历生日月份是不是奇数?
问题2:你是否抽烟?
每个被调查者随机从袋中摸出1个球(摸出后再放回袋中).若摸到红球就如实回答第一个问题,若摸到绿球,则不回答任何问题;若摸到白球,则如实回答第二个问题.所有回答“是”的调查者只需往一个盒子中放一个小石子,回答“否”的被调查者什么也不用做.最后收集回来53个小石子,估计该学校吸烟的人数有多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com