
【题目】在棱长为1的正方体ABCDA1B1C1D1中,E为棱BC的中点,点F是棱CD上的动点,试确定点F的位置,使得D1E⊥平面AB1F. 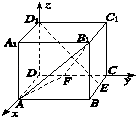
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 经过椭圆
经过椭圆![]()
![]() 的焦点.
的焦点.
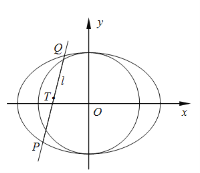
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,
两点,![]() 为弦
为弦![]() 的中点,
的中点,![]() ,记直线
,记直线![]() 的斜率分别为
的斜率分别为![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设定义在R上的偶函数f(x),满足对任意x∈R都有f(t)=f(2﹣t)且x∈(0,1]时,f(x)= ![]() ,a=f(
,a=f( ![]() ),b=f(
),b=f( ![]() ),c=f(
),c=f( ![]() ),用“<“表示a,b,c的大小关系是 .
),用“<“表示a,b,c的大小关系是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
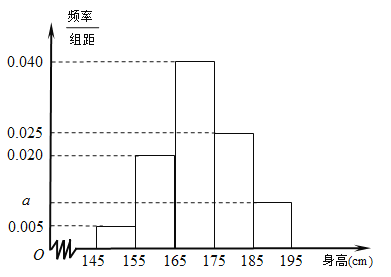
【题目】某中学随机选取了![]() 名男生,将他们的身高作为样本进行统计,得到如图所示的频率分布直方图.观察图中数据,完成下列问题.
名男生,将他们的身高作为样本进行统计,得到如图所示的频率分布直方图.观察图中数据,完成下列问题.
(Ⅰ)求![]() 的值及样本中男生身高在
的值及样本中男生身高在![]() (单位:
(单位: ![]() )的人数;
)的人数;
(Ⅱ)假设同一组中的每个数据可用该组区间的中点值代替,通过样本估计该校全体男生的平均身高;
(Ⅲ)在样本中,从身高在![]() 和
和![]() (单位:
(单位: ![]() )内的男生中任选两人,求这两人的身高都不低于
)内的男生中任选两人,求这两人的身高都不低于![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x+![]() |+a|x﹣
|+a|x﹣![]() |.
|.
(Ⅰ)当a=﹣1时,解不等式f(x)≤3x;
(Ⅱ)当a=2时,若关于x的不等式2f(x)+1<|1﹣b|的解集为空集,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形ABCD是菱形,ADNM是矩形,平面ADNM⊥平面ABCD,∠DAB=60°,AD=2,AM=1,E为AB的中点.
(Ⅰ)求证:AN∥平面MEC;
(Ⅱ)在线段AM上是否存在点P,使二面角P﹣EC﹣D的大小为![]() ?若存在,求出AP的长h;若不存在,请说明理由.
?若存在,求出AP的长h;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧面ABB1A1⊥底面ABC,CA=CB,D,E,F分别为AB,A1D,A1C的中点,点G在AA1上,且A1D⊥EG. 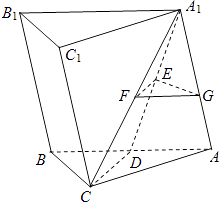
(1)求证:CD∥平面EFG;
(2)求证:A1D⊥平面EFG.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某媒体为了解某地区大学生晚上放学后使用手机上网情况,随机抽取了100名大学生进行调查.如图是根据调查结果绘制的学生每晚使用手机上网平均所用时间的频率分布直方图.将时间不低于40分钟的学生称为“手机迷”. 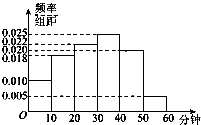
(1)样本中“手机迷”有多少人?
(2)根据已知条件完成下面的2×2列联表,并据此资料判断是否有95%的把握认为“手机迷”与性别有关?
(3)将上述调查所得到的频率视为概率.现在从该地区大量大学 生中,采用随机抽样方法每次抽取1名大学生,抽取3次,经调查一名“手机迷”比“非手机迷”每月的话费平均多40元,记被抽取的3名大学生中的“手机迷”人数为X,且设3人每月的总话费比“非手机迷”共多出Y元,若每次抽取的结果是相互独立的,求X的分布列和Y的期望EY
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com