
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,直线y=k(x+1)与C相切于点A,|AF|=2.
(Ⅰ)求抛物线C的方程;
(Ⅱ)设直线l交C于M,N两点,T是MN的中点,若|MN|=8,求点T到y轴距离的最小值及此时直线l的方程.
【答案】(Ⅰ)y2=4x(Ⅱ)T到y轴的距离的最小值为3,此时直线的方程为x±y-1=0.
【解析】
(Ⅰ)设A(x0,y0),联立直线方程和抛物线方程,运用判别式为0,结合抛物线的定义,可得抛物线方程;
(Ⅱ)由题意可得直线l的斜率不为0,设l:x=my+n,M(x1,y1),N(x2,y2),联立抛物线方程,运用韦达定理和弦长公式,结合中点坐标公式和基本不等式可得所求直线方程.
(Ⅰ)设A(x0,y0),直线y=k(x+1)代入y2=2px,
可得k2x2+(2k2-2p)x+k2=0,
由△=(2k2-2p)2-4k4=0,解得p=2k2,解得x0=1,
由|AF|=1+![]() =2,即p=2,
=2,即p=2,
可得抛物线方程为y2=4x;
(Ⅱ)由题意可得直线l的斜率不为0,设l:x=my+n,M(x1,y1),N(x2,y2),
联立抛物线方程可得y2-4my-4n=0,
△=16m2+16n>0,y1+y2=4m,y1y2=-4n,
|AB|=![]()
![]() =8,
=8,
可得n=![]() -m2,
-m2,
![]() =2m,
=2m,![]() =
=![]() =2m2+n=
=2m2+n=![]() +m2
+m2
=![]() +m2+1-1≥2
+m2+1-1≥2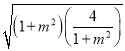 -1=3,
-1=3,
当且仅当![]() =m2+1,即m2=1,即m=±1,
=m2+1,即m2=1,即m=±1,
T到y轴的距离的最小值为3,
此时n=1,直线的方程为x±y-1=0..


科目:高中数学 来源: 题型:
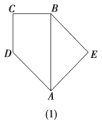
【题目】已知直角梯形![]() 的下底与等腰直角三角形
的下底与等腰直角三角形![]() 的斜边重合,
的斜边重合,![]() 且
且![]() (如图(1)所示),将此图形沿
(如图(1)所示),将此图形沿![]() 折叠成直二面角,连接
折叠成直二面角,连接![]() ,
,![]() ,得到四棱锥
,得到四棱锥![]() (如图(2)所示).
(如图(2)所示).
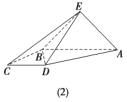
(1)线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() ;若不存在,说明理由;
;若不存在,说明理由;
(2)在(1)的条件下,求平面![]() 与平面
与平面![]() 的夹角的余弦值.
的夹角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市环保部门对市中心每天的环境污染情况进行调查研究后,发现一天中环境综合污染指数![]() 与时刻
与时刻![]() (时)的关系为
(时)的关系为![]() ,
,![]() ,其中
,其中![]() 是与气象有关的参数,且
是与气象有关的参数,且![]() .若用每天
.若用每天![]() 的最大值为当天的综合污染指数,并记作
的最大值为当天的综合污染指数,并记作![]() .
.
(1)令![]() ,
,![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)求![]() 的表达式,并规定当
的表达式,并规定当![]() 时为综合污染指数不超标,求当
时为综合污染指数不超标,求当![]() 在什么范围内时,该市市中心的综合污染指数不超标.
在什么范围内时,该市市中心的综合污染指数不超标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在5件产品中,有3件一等品和2件二等品,从中任取2件,以![]() 为概率的事件是( )
为概率的事件是( )
A. 恰有1件一等品 B. 至少有一件一等品
C. 至多有一件一等品 D. 都不是一等品
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】语文成绩服从正态分布![]() ,数学成绩的频率分布直方图如图:
,数学成绩的频率分布直方图如图:

(1)如果成绩大于135的为特别优秀,这500名学生中本次考试语文、数学特别优秀的大约各多少人?
(2)如果语文和数学两科都特别优秀的共有6人,从(1)中的这些同学中随机抽取3人,设三人中两科都特别优秀的有![]() 人,求
人,求![]() 的分布列和数学期望.
的分布列和数学期望.
(3)根据以上数据,是否有99%的把握认为语文特别优秀的同学,数学也特别优秀.
①若![]() ,则
,则![]() ,
,![]() .
.
②
③
| 0.050 | 0.040 | … | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | … | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着改革开放的不断深入,祖国不断富强,人民的生活水平逐步提高,为了进一步改善民生,2019年1月1日起我国实施了个人所得税的新政策,其政策的主要内容包括:(1)个税起征点为5000元;(2)每月应纳税所得额(含税)![]() 收入
收入![]() 个税起征点
个税起征点![]() 专项附加扣除;(3)专项附加扣除包括①赡养老人费用②子女教育费用③继续教育费用④大病医疗费用
专项附加扣除;(3)专项附加扣除包括①赡养老人费用②子女教育费用③继续教育费用④大病医疗费用![]() 等.其中前两项的扣除标准为:①赡养老人费用:每月扣除2000元②子女教育费用:每个子女每月扣除1000元.新个税政策的税率表部分内容如下:
等.其中前两项的扣除标准为:①赡养老人费用:每月扣除2000元②子女教育费用:每个子女每月扣除1000元.新个税政策的税率表部分内容如下:
级数 | 一级 | 二级 | 三级 | 四级 |
|
每月应纳税所得额(含税) | 不超过3000元的部分 | 超过3000元至12000元的部分 | 超过12000元至25000元的部分 | 超过25000元至35000元的部分 |
|
税率 | 3 | 10 | 20 | 25 |
|
(1)现有李某月收入29600元,膝下有一名子女,需要赡养老人,除此之外,无其它专项附加扣除.请问李某月应缴纳的个税金额为多少?
(2)为研究月薪为20000元的群体的纳税情况,现收集了某城市500名的公司白领的相关资料,通过整理资料可知,有一个孩子的有400人,没有孩子的有100人,有一个孩子的人中有300人需要赡养老人,没有孩子的人中有50人需要赡养老人,并且他们均不符合其它专项附加扣除(受统计的500人中,任何两人均不在一个家庭).若他们的月收入均为20000元,依据样本估计总体的思想,试估计在新个税政策下这类人群缴纳个税金额![]() 的分布列与期望.
的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标平面内,直线l过点P(1,1),且倾斜角α=![]() .以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知圆C的极坐标方程为ρ=4sin θ.
.以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知圆C的极坐标方程为ρ=4sin θ.
(1)求圆C的直角坐标方程;
(2)设直线l与圆C交于A,B两点,求|PA|·|PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了![]() 名观众进行调查,如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图,将日均收看该体育节目时间不低于
名观众进行调查,如图是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图,将日均收看该体育节目时间不低于![]() 分钟的观众称为体育迷.
分钟的观众称为体育迷.
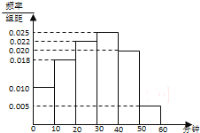
(1)若日均收看该体育节目时间在![]() 内的观众中恰有两名女性,现日均收看时间在
内的观众中恰有两名女性,现日均收看时间在![]() 内的观众中抽取两名进行调查,求这两名观众恰好一男一女的概率;
内的观众中抽取两名进行调查,求这两名观众恰好一男一女的概率;
(2)若抽取![]() 人中有女性
人中有女性![]() 人,其中女体育迷有
人,其中女体育迷有![]() 人,完成答题卡中的列联表并判断能否在犯错误概率不超过
人,完成答题卡中的列联表并判断能否在犯错误概率不超过![]() 的前提下认为体育迷与性别有关系?
的前提下认为体育迷与性别有关系?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 |
|
| |
合计 |
附表及公式: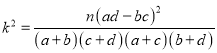 ,
,![]()
k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近几年,我国在电动汽车领域有了长足的发展,电动汽车的核心技术是动力总成,而动力总成的核心技术是电机和控制器,我国永磁电机的技术已处于国际领先水平.某公司计划今年年初用196万元引进一条永磁电机生产线,第一年需要安装、人工等费用24万元,从第二年起,包括人工、维修等费用每年所需费用比上一年增加8万元,该生产线每年年产值保持在100万元.
(1)引进该生产线几年后总盈利最大,最大是多少万元?
(2)引进该生产线几年后平均盈利最多,最多是多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com