
����Ŀ��ij����Ϊ���ijƷ�ֻ�����������չ�������»����![]() ʵ��طֱ��üס��ҷ�����ѵ��Ʒ�ֻ���.Ϊ�۲�������������ֱ���ʵ��������ȡ��
ʵ��طֱ��üס��ҷ�����ѵ��Ʒ�ֻ���.Ϊ�۲�������������ֱ���ʵ��������ȡ��![]() �꣬��ÿ������ۺ����֣���ÿ�����õ��ۺ������Ƴ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ.���ۺ�����Ϊ
�꣬��ÿ������ۺ����֣���ÿ�����õ��ۺ������Ƴ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ.���ۺ�����Ϊ![]() �����ϵĻ���Ϊ���ʻ���.
�����ϵĻ���Ϊ���ʻ���.

![]() ��ͼ��
��ͼ��![]() ��ֵ�������ۺ����ֵ���λ��.
��ֵ�������ۺ����ֵ���λ��.
![]() �������������壬��Ƶ����Ϊ���ʣ�����
�������������壬��Ƶ����Ϊ���ʣ�����![]() ��������������ȡ
��������������ȡ![]() �û��磬������ȡ�Ļ����е����ʻ������ķֲ��к���ѧ������
�û��磬������ȡ�Ļ����е����ʻ������ķֲ��к���ѧ������
![]() ��д����������������ж��Ƿ���
��д����������������ж��Ƿ���![]() �İ�����Ϊ���ʻ��������������й�.
�İ�����Ϊ���ʻ��������������й�.
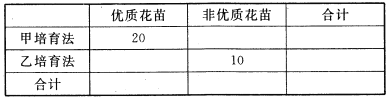
����������ٽ�ֵ�������ο�.
![]()
���ο���ʽ��![]() ������
������![]() .��
.��
���𰸡���1��82.5����2������������3����![]() �İ�����Ϊ���ʻ��������������й�ϵ.
�İ�����Ϊ���ʻ��������������й�ϵ.
��������
��1������Ƶ��֮��Ϊ1�õ�![]() �����������ȣ������λ��.
�����������ȣ������λ��.
��2�����ö���ֲ��г���Ӧ�ĸ��ʣ�д���ֲ��У������ѧ����.
��3���������ʻ����������ñ���ѡȡ��Ӧ���ݣ�����õ�![]() ���ٽ����ж�.
���ٽ����ж�.
![]() ��
��![]() ��
��
���![]()
��÷���λ��Ϊ![]() ����
����![]() ���
���![]()
���ۺ����ֵ���λ��Ϊ![]()
![]() ��
��![]() ��Ƶ�ʷֲ�ֱ�����ʻ����Ƶ��Ϊ
��Ƶ�ʷֲ�ֱ�����ʻ����Ƶ��Ϊ![]() ��������Ϊ
��������Ϊ![]() ��
��
������ȡ�Ļ���Ϊ���ʻ���Ŀ���Ϊ![]() ����
����![]() �����ǣ�
�����ǣ�
![]()
![]() ��ֲ���Ϊ��
��ֲ���Ϊ��

���ԣ�����ȡ�Ļ���Ϊ���ʻ������ѧ����![]()
![]() ���
���![]() ��Ƶ�ʷֲ�ֱ��ͼ�����ʻ����Ƶ��Ϊ
��Ƶ�ʷֲ�ֱ��ͼ�����ʻ����Ƶ��Ϊ![]() ���������֣����ʻ���Ŀ���Ϊ
���������֣����ʻ���Ŀ���Ϊ![]() �ã����������±���ʾ��
�ã����������±���ʾ��

�ɵ�![]()
���ԣ���![]() �İ�����Ϊ���ʻ��������������й�ϵ.
�İ�����Ϊ���ʻ��������������й�ϵ.


 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д� â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������
������![]() Ϊ��Ȼ�����ĵ�����.
Ϊ��Ȼ�����ĵ�����.
��1����![]() ,����
,����![]() ������
������![]() �ϵ����ֵ��
�ϵ����ֵ��
��2����![]() ,����
,����![]() �ķ���
�ķ���![]() ���ҽ���һ����, ��ʵ��
���ҽ���һ����, ��ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����������![]() ,����ʽ
,����ʽ![]() ������, ��ʵ��
������, ��ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC��![]() ��������Ϊ
��������Ϊ![]() ����Բ�����ҽ���ֱ�ΪF1��F2����MΪ��Բ�ϵ�һ�����㣬��MF1F2��������ֵΪ
����Բ�����ҽ���ֱ�ΪF1��F2����MΪ��Բ�ϵ�һ�����㣬��MF1F2��������ֵΪ![]() ������Բ��һ�㣨m��0����m��a������б��Ϊ
������Բ��һ�㣨m��0����m��a������б��Ϊ![]() ��ֱ��l����Բ��C��D���㣮
��ֱ��l����Բ��C��D���㣮
��1������Բ�ķ��̣�
��2����![]() ����m��ֵ��
����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ֱ��l1��ax��by��4��0��l2��(a��1)x��y��b��0.��ֱ���������������a��b��ֵ��
(1)ֱ��l1����(��3����1)������ֱ��l1��l2��ֱ��
(2)ֱ��l1��ֱ��l2ƽ�У���������ԭ�㵽l1��l2�ľ�����ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ָ��![]() ��һ�ַ�ӳ�����ۿ��������ķ�����
��һ�ַ�ӳ�����ۿ��������ķ�����![]() ָ�������������Ӧ���±���ʾ��
ָ�������������Ӧ���±���ʾ��

��ͼ��ij����2018��12��ȫ�µ�ָ![]() ���仯ͳ��ͼ.
���仯ͳ��ͼ.
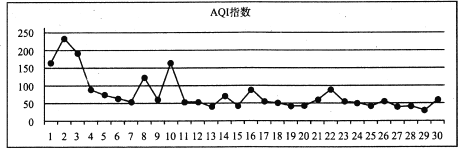
����ͳ��ͼ�жϣ����н�����ȷ���ǣ� ��
A. �����Ͽ�������µĿ�������Խ��Խ��
B. �����Ͽ���ǰ���µĿ����������ں���µĿ�������
C. ��![]() ���ݿ���ǰ���µķ�����ں���µķ���
���ݿ���ǰ���µķ�����ں���µķ���
D. ��![]() ���ݿ���ǰ���µ�ƽ��ֵС�ں���µ�ƽ��ֵ
���ݿ���ǰ���µ�ƽ��ֵС�ں���µ�ƽ��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
��![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ��
Ϊ��![]() ���е�.
���е�.
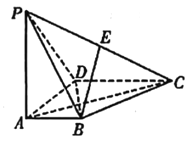
��1��֤����![]() ��
��![]() ��
��
��2��֤������![]() ��
��![]() ��
��
��3����ֱ��![]() ����
����![]() ���ɽǵ�����ֵ.
���ɽǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x����2x3��3ax2+1��
��1����a����1������f��x���ĵ������䣻
��2��������f��x������ֻ��2����ͬ����㣬��ʵ��a��ֵ��
��3��������y��|f��x��|��[0��1]�ϵ���Сֵ��0����ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����μ���ѧ��һ���Բ�������̬Ϊ�о�����ļ���ѧ�����ε�����ṹ��Ϊ���ӣ������ڲ�ȴ���й��ɿ�Ѱ�ģ�һ����ѧ�����Ϸ��ε������ǻ���һ�����ϵ����ķ���ʽ����һ�ֻ��ڵݹ�ķ���ϵͳ�����������÷��εķ������õ�һϵ��ͼ�Σ���ͼ1���߶�![]() �ij���Ϊa�����߶�
�ij���Ϊa�����߶�![]() ��ȡ������
��ȡ������![]() ��
��![]() ��ʹ��
��ʹ��![]() ����
����![]() Ϊһ�����߶�
Ϊһ�����߶�![]() ���Ϸ���һ���������Σ�Ȼ��ȥ���߶�
���Ϸ���һ���������Σ�Ȼ��ȥ���߶�![]() ���õ�ͼ2�е�ͼ�Σ���ͼ2�е����Ϸ����߶�
���õ�ͼ2�е�ͼ�Σ���ͼ2�е����Ϸ����߶�![]() ����ͬ�IJ������õ�ͼ3�е�ͼ�Σ��������ƣ����Ǿ͵õ�������һϵ��ͼ�Σ�
����ͬ�IJ������õ�ͼ3�е�ͼ�Σ��������ƣ����Ǿ͵õ�������һϵ��ͼ�Σ�

�ǵ�![]() ��ͼ�Σ�ͼ1Ϊ��1��ͼ�Σ��е������߶γ��ĺ�Ϊ
��ͼ�Σ�ͼ1Ϊ��1��ͼ�Σ��е������߶γ��ĺ�Ϊ![]() ���ָ����й�����
���ָ����й�����![]() ���ĸ����⣺
���ĸ����⣺
������![]() �ǵȱ����У�
�ǵȱ����У�
������![]() �ǵ������У�
�ǵ������У�
�۴�����С������![]() ��ʹ�ö������������
��ʹ�ö������������![]() ������
������![]() ��
��
�ܴ�����������![]() ��ʹ�ö������������
��ʹ�ö������������![]() ������
������![]() ��
��
����������������________________����д���������������ţ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�����ֱ��
�У�����ֱ��![]() �͵�
�͵�![]() ��
��![]() ����
����![]() ����
����![]() ����Ƶ�
����Ƶ�![]() ,
,![]() ��ֱ��l�ָ���������C��ֱ��lû�й����㣬������C�ϴ��ڵ�
��ֱ��l�ָ���������C��ֱ��lû�й����㣬������C�ϴ��ڵ�![]() ,
,![]() ��ֱ��l�ָ������ֱ��lΪ����C��һ���ָ���.
��ֱ��l�ָ������ֱ��lΪ����C��һ���ָ���.
��1����֤����![]() ��
��![]() ��ֱ��
��ֱ��![]() �ָ���
�ָ���
��2����ֱ��![]() ������
������![]() �ķָ��ߣ���ʵ��
�ķָ��ߣ���ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3������M����![]() �ľ����뵽y��ľ���֮��Ϊ1�����M�Ĺ켣ΪE����E�ķ��̣���֤��y��Ϊ����E�ķָ���.
�ľ����뵽y��ľ���֮��Ϊ1�����M�Ĺ켣ΪE����E�ķ��̣���֤��y��Ϊ����E�ķָ���.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com