
【题目】根据中国生态环境部公布的2017年、2018年长江流域水质情况监测数据,得到如下饼图:
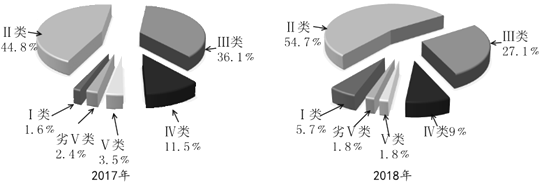
则下列说法错误的是( )
A.2018年的水质情况好于2017年的水质情况
B.2018年与2017年相比较,Ⅰ、Ⅱ类水质的占比明显增加
C.2018年与2017年相比较,占比减小幅度最大的是Ⅳ类水质
D.2018年Ⅰ、Ⅱ类水质的占比超过![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某销售公司拟招聘一名产品推销员,有如下两种工资方案:
方案一:每月底薪2000元,每销售一件产品提成15元;
方案二:每月底薪3500元,月销售量不超过300件,没有提成,超过300件的部分每件提成30元.
(1)分别写出两种方案中推销员的月工资![]() (单位:元)与月销售产品件数
(单位:元)与月销售产品件数![]() 的函数关系式;
的函数关系式;
(2)从该销售公司随机选取一名推销员,对他(或她)过去两年的销售情况进行统计,得到如下统计表:
月销售产品件数 | 300 | 400 | 500 | 600 | 700 |
次数 | 2 | 4 | 9 | 5 | 4 |
把频率视为概率,分别求两种方案推销员的月工资超过11090元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学成就的杰出代表作之一,其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积![]() (弦
(弦![]() 矢
矢![]() 矢
矢![]() ),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为
),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为![]() ,半径等于6米的弧田,按照上述经验公式计算所得弧田面积约为( )
,半径等于6米的弧田,按照上述经验公式计算所得弧田面积约为( )
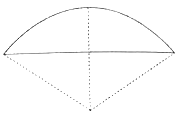
A.12平方米B.16平方米C.20平方米D.24平方米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大豆,古称菽,原产中国,在中国已有五千年栽培历史.2019年春,为响应中国大豆参与世界贸易的竞争,某市农科院积极研究,加大优良品种的培育工作,其中一项基础工作就是研究昼夜温差大小与大豆发芽率之间的关系.为此科研人员分别记录了7天中每天50粒大豆的发芽数得如下数据表格:
日期 | 4月3日 | 4月4日 | 4月5日 | 4月6日 | 4月7日 | 4月8日 | 4月9日 |
温差 | 8 | 9 | 10 | 12 | 11 | 8 | 13 |
发芽数 | 21 | 25 | 26 | 32 | 27 | 20 | 33 |
科研人员确定研究方案是:从7组数据中选5组数据求线性回归方程,再用求得的回归方程对剩下的2组数据进行检验.
(1)若选取的是4月4日至4月8日五天数据,据此求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若由线性回归方程得到的估计数据与实际数据的误差绝对值均不超过1粒,则认为得到的线性回归方程是可靠的,请检验(1)中回归方程是否可靠?
注: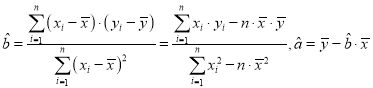 .
.
参考数值:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.
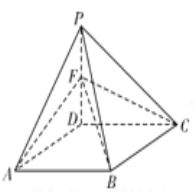
(Ⅰ)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,并说明理由;
,并说明理由;
(Ⅱ)当二面角![]() 的余弦值为
的余弦值为![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成的角.
所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设![]() ,
,![]() 分别是正方体
分别是正方体![]() 的棱
的棱![]() 上两点,且
上两点,且![]() ,
,![]() ,其中正确的命题为( )
,其中正确的命题为( )
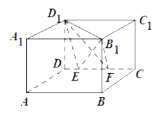
A.三棱锥![]() 的体积为定值
的体积为定值
B.异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
C.![]() 平面
平面![]()
D.直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2018年俄罗斯世界杯期间,莫斯科的部分餐厅经营了来自中国的小龙虾,这些小龙虾标有等级代码.为得到小龙虾等级代码数值![]() 与销售单价
与销售单价![]() 之间的关系,经统计得到如下数据:
之间的关系,经统计得到如下数据:
等级代码数值 | 38 | 48 | 58 | 68 | 78 | 88 |
销售单价 | 16.8 | 18.8 | 20.8 | 22.8 | 24 | 25.8 |
(1)已知销售单价![]() 与等级代码数值
与等级代码数值![]() 之间存在线性相关关系,求
之间存在线性相关关系,求![]() 关于
关于![]() 的线性回归方程(系数精确到0.1);
的线性回归方程(系数精确到0.1);
(2)若莫斯科某个餐厅打算从上表的6种等级的中国小龙虾中随机选2种进行促销,记被选中的2种等级代码数值在60以下(不含60)的数量为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式:对一组数据![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距最小二乘估计分别为:
的斜率和截距最小二乘估计分别为: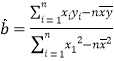 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com