
【题目】已知f(x)= ![]() ,g(x)=
,g(x)= ![]() .
.
(1)当1≤x<2时,求g(x);
(2)当x∈R时,求g(x)的解析式,并画出其图象; 
(3)求方程xf[g(x)]=2g[f(x)]的解.
 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
【题目】雾霾天气对城市环境造成很大影响,按照国家环保部发布的标准:居民区的PM2.5(大气中直径小于或等于2.5微米的颗粒物)年平均浓度不得超过35微克/立方米.某市环保部门加强了对空气质量的监测,抽取某居民区监测点的20天PM2.5的24小时平均浓度的监测数据,制成茎叶图,如图:
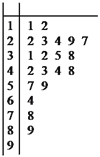
(Ⅰ)完成如下频率分布表,并在所给的坐标系中画出![]() 的频率分布直方图;
的频率分布直方图;
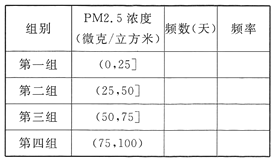
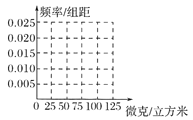
(Ⅱ)从样本中PM2.5的24小时平均浓度超过50微克/立方米的天数中,随机抽取2天,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的方程为: ![]() =1(a>0),其焦点在x轴上,离心率e=
=1(a>0),其焦点在x轴上,离心率e= ![]() .
.
(1)求该椭圆的标准方程;
(2)设动点P(x0 , y0)满足 ![]() ,其中O为坐标原点,M,N是椭圆C上的点,直线OM与ON的斜率之积为﹣
,其中O为坐标原点,M,N是椭圆C上的点,直线OM与ON的斜率之积为﹣ ![]() ,求证:x02+2y02为定值.
,求证:x02+2y02为定值.
(3)在(2)的条件下,问:是否存在两个定点A,B,使得|PA|+|PB|为定值?若存在,给出证明;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图 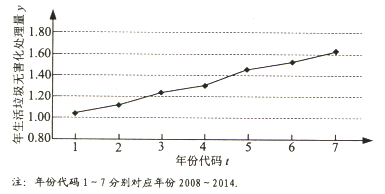
(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2017年我国生活垃圾无害化处理量.
参考数据: ![]() =9.32,
=9.32, ![]() yi=40.17,
yi=40.17, ![]() =0.55,
=0.55, ![]() ≈2.646.
≈2.646.
参考公式:相关系数r= 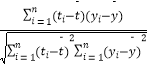 回归方程
回归方程 ![]() =
= ![]() +
+ ![]() t 中斜率和截距的最小二乘估计公式分别为:
t 中斜率和截距的最小二乘估计公式分别为: ![]() =
= 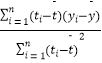 ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC—A1B1C1中,AB=BC=BB1, ![]() ,D为AC上的点,B1C∥平面A1BD;
,D为AC上的点,B1C∥平面A1BD;
(1)求证:BD⊥平面![]() ;
;
(2)若![]() 且
且![]() ,求三棱锥A-BCB1的体积.
,求三棱锥A-BCB1的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A、B、C所对边分别是a、b、c,已知B=60°,
(1)若b= ![]() ,A=45°,求a;
,A=45°,求a;
(2)若a、b、c成等比数列,请判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+2x.
(1)现已画出函数f(x)在y轴左侧的图象,如图所示,请补出完整函数f(x)的图象,并根据图象写出函数f(x)的增区间; 
(2)写出函数f(x)的解析式和值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,且,
,且, ![]() ,
, ![]() ,
, ![]() 为线段
为线段![]() 上一点,
上一点, ![]() ,且
,且![]() 为
为![]() 的中点.
的中点.
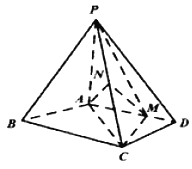
(Ⅰ)证明: ![]() 平面
平面![]() ;
;
(Ⅱ)求证:平面![]() 平面
平面![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2﹣2ax+b+1(a>0)在区间[2,3]上有最大值4,最小值1.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)设g(x)= ![]() .若不等式g(2x)﹣k2x≥0对任意x∈[1,2]恒成立,求k的取值范围.
.若不等式g(2x)﹣k2x≥0对任意x∈[1,2]恒成立,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com