
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���ԲE�� ![]() =1��a��b��0���Ľ���Ϊ2���ҹ��㣨
=1��a��b��0���Ľ���Ϊ2���ҹ��㣨 ![]() ��
�� ![]() ����
���� 
��1������ԲE�ķ��̣�
��2������A��B�ֱ�����ԲE�����Ҷ��㣬ֱ��l������B�Ҵ�ֱ��x�ᣬ��P����Բ������A��B������һ�㣬ֱ��AP��l�ڵ�M�� ����ֱ��OM��б��Ϊk1 �� ֱ��BP��б��Ϊk2 �� ��֤��k1k2Ϊ��ֵ��
�������M��ֱ��PB��ֱ��Ϊm����֤��ֱ��m�����㣬�������������꣮
���𰸡�
��1���⣺��������ԲE�� ![]() =1��a��b��0���Ľ���Ϊ2���ҹ��㣨
=1��a��b��0���Ľ���Ϊ2���ҹ��㣨 ![]() ��
�� ![]() ����
����
��c=1�� ![]()
����a=2��b= ![]() ��
��
����ԲE�ı�����Ϊ ![]()
��2���⣺����P��x0��y0����y0��0����
��ֱ��AP�ķ���Ϊ��y= ![]() ��x+2��
��x+2��
��x=2��M��2�� ![]() ��
��
��k1= ![]() ��
��
��k2= ![]() ��
��
��k1k2= ![]() ��
��
��P��x0��y0������Բ�ϣ��� ![]() =1
=1
��k1k2=�� ![]() Ϊ��ֵ��
Ϊ��ֵ��
��ֱ��BP��б��Ϊ ![]() ��ֱ��m��б��Ϊkm=
��ֱ��m��б��Ϊkm= ![]() ��
��
��ֱ��m�ķ���Ϊy= ![]() ��x��2��+y0=
��x��2��+y0= ![]() ��x��2��+
��x��2��+ ![]() =
= ![]() ��x+1����
��x+1����
����ֱ��m�����㣨��1��0��
����������1��������c=1�� ![]() ��������ɣ���2������P��x0 �� y0����y0��0�������ɵó�ֱ��AP�ķ��̣���x=2�����ɵõ���M�����꣬����б�ʼ��㹫ʽ���ɵó�k1 �� k2 �� �����õ�P����Բ�ϼ���֤����������ֱ�ߵĵ�бʽ����ٵ��йؽ��ۼ���֤����
��������ɣ���2������P��x0 �� y0����y0��0�������ɵó�ֱ��AP�ķ��̣���x=2�����ɵõ���M�����꣬����б�ʼ��㹫ʽ���ɵó�k1 �� k2 �� �����õ�P����Բ�ϼ���֤����������ֱ�ߵĵ�бʽ����ٵ��йؽ��ۼ���֤����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������P��ABCD�У�PA=AB=a��E����PC���е㣮 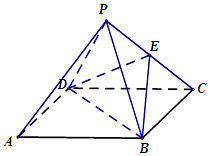
��1����֤��PC��BD��
��2����ֱ��BE��PA���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���� ![]() ��a��bΪʵ��������
��a��bΪʵ��������
��1����a=b=1ʱ��֤����f��x�������溯����
��2����f��x�����溯������a��b��ֵ��
��3����f��x�����溯��ʱ���о��Ƿ����������ʵ�������Ӽ�D�����κ�����D��x��c������f��x����c2��3c+3���������������ҳ�����������D���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ�ij����ͼ��ʾ���㷨�У���������ʵ��a��b��c��Ҫ�������x����������������������ô�ڿհ��жϿ��У�Ӧ�����루 �� 
A.x��c
B.c��x
C.c��b
D.c��a
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ʵ��x��y���㲻��ʽ��  ����Ŀ�꺯��z=kx+y���ڵ㣨1��1����ȡ����Сֵ����ʵ��k��ȡֵ��Χ�� �� ��
����Ŀ�꺯��z=kx+y���ڵ㣨1��1����ȡ����Сֵ����ʵ��k��ȡֵ��Χ�� �� ��
A.����1��+�ޣ�
B.�����ޣ���1��
C.��1��+�ޣ�
D.�����ޣ�1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=sinxcos2x�������н����д����Ϊ�� ��
A.�㣨�У�0���Ǻ���y=f��x��ͼ���һ���Գ�����
B.ֱ��x= ![]() �Ǻ���y=f��x��ͼ���һ���Գ���
�Ǻ���y=f��x��ͼ���һ���Գ���
C.���Ǻ���y=f��x��������
D.����y=f��x�������ֵΪ1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ԲC�� ![]() +
+ ![]() =1��a��b��0������ΪF1����1��0������������e���㣨1��e������Բ�ϣ�
=1��a��b��0������ΪF1����1��0������������e���㣨1��e������Բ�ϣ� 
��1������ԲC�ķ��̣�
��2�����M��2��0��������F1��ֱ�߽�C��A��B���㣬ֱ��MA��MB��ֱ��x=��2�ֱ���P��Q���㣬���MPQ��������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������R�ϵĺ���y=f��x�����㣺����y=f��x+1����ͼ�����ֱ��x=��1�Գƣ��ҵ�x�ʣ����ޣ�0��ʱ��f��x��+xf�䣨x����0������f�䣨x���Ǻ���f��x���ĵ�����������a=0.76f��0.76����b=log ![]() 6f��log
6f��log ![]() 6����c=60.6f��60.6������a��b��c�Ĵ�С��ϵ�ǣ� ��
6����c=60.6f��60.6������a��b��c�Ĵ�С��ϵ�ǣ� ��
A.a��b��c
B.b��a��c
C.c��a��b
D.a��c��b
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У��ڽ�A��B��C�ĶԱ߷ֱ�Ϊa��b��c����֪a=bcosC+csinB��b=2�����ABC��������ֵΪ ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com