
【题目】“北祠堂”是我校著名的一支学生乐队,对于2015年我校“校园周末文艺广场”活动中“北祠堂”乐队的表现,在高一年级学生中投票情况的统计结果见表:
喜爱程度 | 非常喜欢 | 一般 | 不喜欢 |
人数 | 500 | 200 | 100 |
现采用分层抽样的方法从所有参与对“北祠堂”投票的800名学生中抽取一个容量为n的样本,若从不喜欢“北祠堂”的100名学生中抽取的人数是5人.
(1)求n的值;
(2)若从不喜欢“北祠堂”的学生中抽取的5人中恰有3名男生(记为a1 , a2 , a3)2名女生(记为b1 , b2),现将此5人看成一个总体,从中随机选出2人,列出所有可能的结果;
(3)在(2)的条件下,求选出的2人中至少有1名女生的概率.
科目:高中数学 来源: 题型:
【题目】如图所示的程序框图表示的算法功能是( )
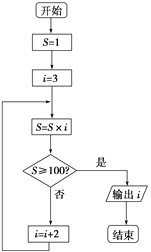
A. 计算小于100的奇数的连乘积
B. 计算从1开始的连续奇数的连乘积
C. 从1开始的连续奇数的连乘积,当乘积大于或等于100时,计算奇数的个数
D. 计算1×3×5×…×n≥100时的最小的n的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2016高考天津文数】某化肥厂生产甲、乙两种混合肥料,需要A,B,C三种主要原料.生产1车皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如下表所示:
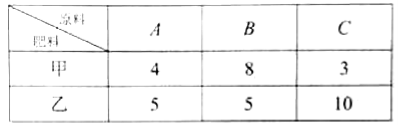
现有A种原料200吨,B种原料360吨,C种原料300吨,在此基础上生产甲、乙两种肥料.已知生产1车皮甲种肥料,产生的利润为2万元;生产1车皮乙种肥料,产生的利润为3万元.分别用x,y计划表示生产甲、乙两种肥料的车皮数.
(Ⅰ)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(Ⅱ)问分别生产甲、乙两种肥料各多少车皮,能够产生最大的利润?并求出此最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店会员活动日.
(Ⅰ)随机抽取50名会员对商场进行综合评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100].
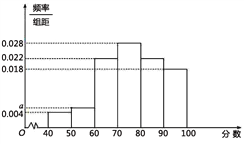
(1)求频率分布直方图中的值;
(2)估计会员对商场的评分不低于80的概率.
(Ⅱ)采取摸球兑奖的方式对会员进行返代金券活动,每位会员从一个装有5个标有面值的球(2个所标的面值为300元,其余3个均为100元)的袋中一次性随机摸出2个球,球上所标的面值之和为该会员所获的代金券金额.求某会员所获得奖励超过400元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得 ![]() ,
, ![]() =20,
=20, ![]() =184,
=184, ![]() =720.
=720.
(1)求家庭的月储蓄y关于月收入x的线性回归方程 ![]() ;
;
(2)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:回归直线的斜率和截距的最小二乘法估计公式分别为: ![]() =
= 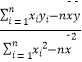 ,
, ![]() =
= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等比数列![]() 中,
中, ![]() ,且
,且![]() 的等比中项为
的等比中项为![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,是否存在正整数
,是否存在正整数![]() ,使得
,使得![]() 对任意
对任意![]() 恒成立?若存在,求出正整数
恒成立?若存在,求出正整数![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(其中ω>0|φ|< ![]() )图象相邻对称轴的距离为
)图象相邻对称轴的距离为 ![]() ,一个对称中心为(﹣
,一个对称中心为(﹣ ![]() ,0),为了得到g(x)=cosωx的图象,则只要将f(x)的图象( )
,0),为了得到g(x)=cosωx的图象,则只要将f(x)的图象( )
A.向右平移 ![]() 个单位
个单位
B.向右平移 ![]() 个单位
个单位
C.向左平移 ![]() 个单位
个单位
D.向左平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人约定在中午12时到下午1时之间到某站乘公共汽车,又知这段时间内有4班公共汽车.设到站时间分别为12:15,12:30,12:45,1:00.如果他们约定:
①见车就乘;
②最多等一辆.
试分别求出在两种情况下两人同乘一辆车的概率.假设甲乙两人到达车站的时间是相互独立的,且每人在中午12点到1点的任意时刻到达车站是等可能的.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com