【题目】设函数
，
，
，
，若
，
，使得直线
的斜率为
，则
的最小值为（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】分析：由题意利用二次函数的性质和导函数研究函数的单调性，确定函数
和函数
的最大值和最小值，结合题意得到关于m的不等式组，求解不等式组即可确定m的范围，进一步即可确定m的最小值.
详解：f(x)=-x2-6x+m=-(x+3)2+m+9,x∈[-5,-2]时：
f(x)max=f(-3)=m+9,f(x)min=f(-5)=m+5.
g'(x）=6x2+6x-12=6(x+2)(x-1)，
所以g(x)在区间[-1，1]上单调递减，在区间(1，2]上单调递增，
g(x)min=g(1)=-7-m，g(-1)=13-m，g(2)=4-m，所以g(x)max=13-m.
，
，,使得直线PQ斜率为0，
等价于
，即
，
解得-6≤m≤2.
则
的最小值为
.
本题选择A选项.
科目：高中数学 来源： 题型：
【题目】已知数列{an}的奇数项成等差数列，偶数项成等比数列，且公差和公比都是2，若对满足m+n≤5的任意正整数m，n，均有am+an=am+n成立． （I）求数列{an}的通项公式；
（II）若bn= 
，求数列{bn}的前n项和Tn ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知y＝f(x)是定义域为R的奇函数，当x∈[0，＋∞)时，f(x)＝x2－2x.
(1)写出函数y＝f(x)的解析式
(2)若方程f(x)＝a恰有3个不同的解，求a的取值范围。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知曲线
参数方程为
（
为参数），当
时，曲线上对应的点为
.以原点
为极点，以
轴的正半轴为极轴建立极坐标系，曲线
的极坐标方程为
.
(1)求曲线的普通方程和曲线的直角坐标方程；
(2)设曲线与的公共点为
，求
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
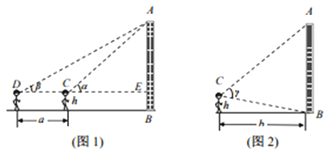
【题目】某校高一数学研究小组测量学校的一座教学楼AB的高度
已知测角仪器距离地面的高度为h米，现有两种测量方法：
方法
如图
用测角仪器，对准教学楼的顶部A，计算并记录仰角
；
后退a米，重复
中的操作，计算并记录仰角
．
方法
如图
用测角仪器，对准教学楼的顶部A底部B，测出教学楼的视角
，测试点与教学楼的水平距离b米．
请你回答下列问题：
用数据
，
，a，h表示出教学楼AB的高度；
按照方法II，用数据
，b，h表示出教学楼AB的高度．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系xOy中，曲线C1： 
（t为参数，t≠0），其中0≤α≤π，在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ=2sinθ，C3：ρ=2 
cosθ．
（1）求C2与C3交点的直角坐标；
（2）若C1与C2相交于点A，C1与C3相交于点B，求|AB|的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}为等差数列，a3=5，a7=13，数列{bn}的前n项和为Sn ， 且有Sn=2bn﹣1．
（1）求{an}、{bn}的通项公式；
（2）若cn=anbn ， {cn}的前n项和为Tn ， 求Tn ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
