
【题目】若![]() 满足
满足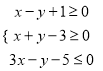 ,求:
,求:
(1)![]() 的最小值;
的最小值;
(2)![]() 的范围;
的范围;
(3)![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:作出约束条件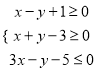 表示的可行域,利用目标函数的几何意义:(1)平移直线可对直线的截距求解最值即可;(2)转化为可行域内的点与原点距离的平方,根据可行域内的点到原点的距离范围求解;(3)转化为可行域内的点与原点直线的斜率与
表示的可行域,利用目标函数的几何意义:(1)平移直线可对直线的截距求解最值即可;(2)转化为可行域内的点与原点距离的平方,根据可行域内的点到原点的距离范围求解;(3)转化为可行域内的点与原点直线的斜率与![]() 的和求解即可.
的和求解即可.
试题解析: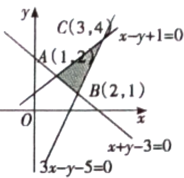
作出满足已知条件的可行域为![]() 内(及边界)区域,其中
内(及边界)区域,其中![]() ,
, ![]() ,
, ![]() .
.
(1)目标函数![]() ,表示直线
,表示直线![]() ,
, ![]() 表示该直线纵截距,当
表示该直线纵截距,当![]() 过点
过点![]() 时纵截距有最小值,故
时纵截距有最小值,故![]() .
.
(2)目标函数![]() 表示区域内的点到坐标系点的距离的平方,又原点
表示区域内的点到坐标系点的距离的平方,又原点![]() 到
到![]() 的距离
的距离![]() 且垂足是
且垂足是![]() 在线段
在线段![]() 上,故
上,故![]() ,即
,即![]()
(3)目标函数![]() ,记
,记![]() .
.
则![]() 表示区域中的点与坐标原点连线的斜率,当直线过点
表示区域中的点与坐标原点连线的斜率,当直线过点![]() 时,斜率最大,即
时,斜率最大,即![]() ,即
,即![]() .
.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分12分,(1)小问7分,(2)小问5分)
设函数![]()
(1)若![]() 在
在![]() 处取得极值,确定
处取得极值,确定![]() 的值,并求此时曲线
的值,并求此时曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若![]() 在
在![]() 上为减函数,求
上为减函数,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为检测空气质量,某市环保局随机抽取了甲、乙两地2016年20天的PM2.5日平均浓度(单位:微克/立方米)是监测数据,得到甲地PM2.5日平均浓度的频率分布直方图和乙地PM2.5日平均浓度的频数分布表.
甲地20天PM2.5日平均浓度频率分布直方图

乙地20天PM2.5日平均浓度频数分布表

(1)根据乙地20天PM2.5日平均浓度的频数分布表作出相应的频率分布直方图,并通过两个频率分布直方图比较两地PM2.5日平均浓度的平均值及分散程度;(不要求计算出具体值,给出结论即可)
(2)求甲地20天PM2.5日平均浓度的中位数;
(3)通过调查,该市市民对空气质量的满意度从高到低分为三个等级:

记事件![]() :“甲地市民对空气质量的满意度等级为不满意”。根据所给数据,利用样本估计总体的统计思想,以事件发生的频率作为相应事件发生的概率,求事件
:“甲地市民对空气质量的满意度等级为不满意”。根据所给数据,利用样本估计总体的统计思想,以事件发生的频率作为相应事件发生的概率,求事件![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知矩形![]() 的长为
的长为![]() ,宽为
,宽为![]() ,
, ![]() 、
、![]() 边分别在
边分别在![]() 轴、
轴、![]() 轴的正半轴上,
轴的正半轴上, ![]() 点与坐标原点重合.将矩形折叠,是
点与坐标原点重合.将矩形折叠,是![]() 点落在线段
点落在线段![]() 上.
上.
(Ⅰ)当![]() 点落在
点落在![]() 中点时,求折痕所在的直线方程.
中点时,求折痕所在的直线方程.
(Ⅱ)若折痕所在直线的斜率为![]() ,求折痕所在的直线方程与
,求折痕所在的直线方程与![]() 轴的交点坐标.(答案中可以出现
轴的交点坐标.(答案中可以出现![]() )
)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位将举办庆典活动,要在广场上竖立一形状为等腰梯形的彩门BADC (如图),设计要求彩门的面积为S (单位:m2)高为h(单位:m)(S,h为常数),彩门的下底BC固定在广场地面上,上底和两腰由不锈钢支架构成,设腰和下底的夹角为α,不锈钢支架的长度和记为l. 
(1)请将l表示成关于α的函数l=f(α);
(2)问当α为何值时l最小?并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知,如图,抛物线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,直线
,直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
, ![]() 两点,点
两点,点![]() 为线段
为线段![]() 中点,直线
中点,直线![]() ,
, ![]() 分别与抛物线切于点
分别与抛物线切于点![]() ,
, ![]() .
.
(![]() )求:线段
)求:线段![]() 的长.
的长.
(![]() )直线
)直线![]() 平行于抛物线
平行于抛物线![]() 的对称轴.
的对称轴.
(![]() )作直线
)作直线![]() 直线
直线![]() ,分别交抛物线
,分别交抛物线![]() 和两条已知切线
和两条已知切线![]() ,
, ![]() 于点
于点![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
求证: ![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 为椭圆
为椭圆![]() :
: ![]() (
(![]() )的左、右焦点,点
)的左、右焦点,点![]() 为椭圆上一点,且
为椭圆上一点,且![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若圆![]() 是以
是以![]() 为直径的圆,直线
为直径的圆,直线![]() :
: ![]() 与圆
与圆![]() 相切,并与椭圆
相切,并与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com