
【题目】已知椭圆![]() 与过其右焦点F(1,0)的直线交于不同的两点A,B,线段AB的中点为D,且直线l与直线OD的斜率之积为
与过其右焦点F(1,0)的直线交于不同的两点A,B,线段AB的中点为D,且直线l与直线OD的斜率之积为![]() .
.
(1)求C的方程;
(2)设椭圆的左顶点为M,kMA,kMB分别表示直线MA,MB的斜率,求证![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)设A,B的坐标,代入椭圆中,两式相减可得直线AB,OD的斜率之积,由题意可得a,b的关系,再由右焦点的坐标及a,b,c之间的关系求出a,b的值,求出椭圆的方程;
(2)由(1)可得M的坐标,将直线l的方程代入椭圆的方程,求出两根之和及两根之积,进而求出直线AM,BM的斜率之和,再由直线AB,OD的斜率之积可证得kAM+kBM![]() kOD.
kOD.
(1)设A(x1,y1),B(x2,y2),D(x0,y0),
将点A,B坐标代入椭圆的方程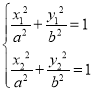 ,两式相减得
,两式相减得![]() 0,
0,
所以kAB![]() ,
,
因为D为AB的中点,所以kOD![]() ,
,
所以kABkOD![]() ,
,
所以![]() ,又a2﹣b2=1,解得:a2=4,b2=3,
,又a2﹣b2=1,解得:a2=4,b2=3,
所以椭圆C的方程为:![]() 1.
1.
(2)由(1)可得左顶点M(﹣2,0),由题意设直线AB的方程:x=my+1,
联立直线与椭圆的方程: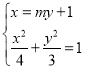 ,整理可得:(4+3m2)y2+6my﹣9=0,
,整理可得:(4+3m2)y2+6my﹣9=0,
所以y1+y2![]() ,y1y2
,y1y2![]() ,
,
所以kAM+kBM![]()
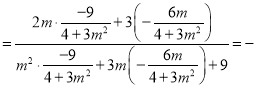 m,
m,
因为kABkOD![]()
![]() kOD
kOD![]() ,所以m
,所以m![]() kOD,即kAM+kBM
kOD,即kAM+kBM![]() kOD.
kOD.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
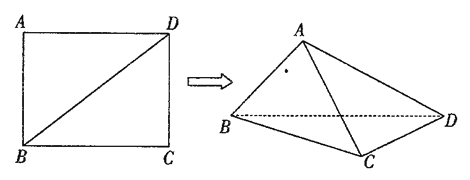
【题目】已知长方形![]() 中,
中,![]() ,
,![]() ,现将长方形沿对角线
,现将长方形沿对角线![]() 折起,使
折起,使![]() ,得到一个四面体
,得到一个四面体![]() ,如图所示.
,如图所示.
(1)试问:在折叠的过程中,异面直线![]() 与
与![]() 能否垂直?若能垂直,求出相应的
能否垂直?若能垂直,求出相应的![]() 的值;若不垂直,请说明理由;
的值;若不垂直,请说明理由;
(2)当四面体![]() 体积最大时,求二面角
体积最大时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆![]()
![]() 的左焦点为
的左焦点为![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() .
.
(1)已知椭圆的离心率为![]() ,线段
,线段![]() 中点的横坐标为
中点的横坐标为![]() ,求椭圆的标准方程;
,求椭圆的标准方程;
(2)已知△![]() 外接圆的圆心在直线
外接圆的圆心在直线![]() 上,求椭圆的离心率
上,求椭圆的离心率![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】癌症是迄今为止人类尚未攻克的疾病之一,目前,癌症只能尽量预防.某医学中心推出了一种抗癌症的制剂,现对20位癌症病人,进行医学试验测试药效,测试结果分为“病人死亡”和“病人存活”,现对测试结果和药物剂量(单位:![]() )进行统计,规定病人在服用
)进行统计,规定病人在服用![]() (包括
(包括![]() )以上为“足量”,否则为“不足量”,统计结果显示,这20病人
)以上为“足量”,否则为“不足量”,统计结果显示,这20病人
中“病人存活”的有13位,对病人服用的药物剂量统计如下表:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
吸收量/ | 6 | 8 | 3 | 8 | 9 | 5 | 6 | 6 | 2 | 7 | 7 | 5 | 10 | 6 | 7 | 8 | 8 | 4 | 6 | 9 |
已知“病人存活”,但服用的药物剂量不足的病人共1位.
(1)完成下列![]() 列联表,并判断是否可以在犯错误的概率不超过1%的前提下,认为“病人存活”与服用药物的剂量足量有关?
列联表,并判断是否可以在犯错误的概率不超过1%的前提下,认为“病人存活”与服用药物的剂量足量有关?
服用药物足量 | 服用药物不足量 | 合计 | |
病人存活 | 1 | ||
病人死亡 | |||
合计 | 20 |
(2)若在该样本“服用药物剂量不足”的病人中随机抽取3位,求这三人中恰有1位“病人存活”的概率.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年冬奥会申办成功,让中国冰雪项目迎来了新的发展机会,“十四冬”作为北京冬奥会前重要的练兵场,对冰雪运动产生了不可忽视的带动作用.某校对冰雪体育社团中甲、乙两人的滑轮、雪合战、雪地足球、冰尜(ga)、爬犁速降及俯卧式爬犁6个冬季体育运动项目进行了指标测试(指标值满分为5分,分高者为优),根据测试情况绘制了如图所示的指标雷达图.则下面叙述正确的是( )
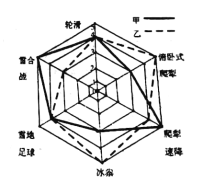
A.甲的轮滑指标高于他的雪地足球指标
B.乙的雪地足球指标低于甲的冰尜指标
C.甲的爬犁速降指标高于乙的爬犁速降指标
D.乙的俯卧式爬犁指标低于甲的雪合战指标
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com