
Ζ÷Έω Θ®1Θ©άϊ”ΟœρΝΩΒΡ ΐΝΩΜΐΙΪ Ϋ«σ≥ωfΘ®xΘ©ΒΡ±μ¥ο ΫΘ§ΫαΚœ»ΐΫ«Κ· ΐΒΡ–‘÷ Ϋχ––«σΫβΦ¥Ω…Θ°
Θ®2Θ©ΗυΨί»ΐΫ«Κ· ΐΒΡΤΫ“ΤΙΊœΒ«σ≥ωgΘ®xΘ©Θ§άϊ”ΟΚ· ΐΒΡΕ‘≥Τ–‘«σ≥ωΕ‘≥ΤΚ· ΐΒΡ±μ¥ο ΫΫχ––«σΫβΦ¥Ω…Θ°
Ϋβ¥π ΫβΘΚΘ®1Θ©ΓΏœρΝΩ$\overrightarrow{a}$=Θ®2sinxΘ§sinx-cosxΘ©Θ§$\overrightarrow{b}$=Θ®cosxΘ§$\sqrt{3}$Θ®cosx+sinxΘ©Θ©Θ§
ΓύfΘ®xΘ©=$\overrightarrow{a}•\overrightarrow{b}$+1=2sinxcosx+$\sqrt{3}$Θ®cosx+sinxΘ©Θ®sinx-cosxΘ©+1
=sin2x-$\sqrt{3}$cos2x+1=2sinΘ®2x-$\frac{Π–}{3}$Θ©+1Θ§
»τx$Γ Θ®\frac{Π–}{4}Θ§\frac{Π–}{2}Θ©$Θ§‘ρ2xΓ Θ®$\frac{Π–}{2}$Θ§Π–Θ©Θ§2x-$\frac{Π–}{3}$Γ Θ®$\frac{Π–}{6}$Θ§$\frac{2Π–}{3}$Θ©Θ§
‘ρ2sinΘ®2x-$\frac{Π–}{3}$Θ©Γ Θ®2sin$\frac{Π–}{6}$Θ§2sin$\frac{Π–}{2}$]Θ§
Φ¥2sinΘ®2x-$\frac{Π–}{3}$Θ©Γ Θ®1Θ§2]Θ§
‘ρ2sinΘ®2x-$\frac{Π–}{3}$Θ©+1Γ Θ®2Θ§3]Θ§
Φ¥Κ· ΐfΘ®xΘ©ΒΡ÷Β”ρΈΣΘ®2Θ§3]Θ§
”…2x-$\frac{Π–}{3}$=kΠ–Θ§ΒΟx=$\frac{kΠ–}{2}$+$\frac{Π–}{6}$Θ§kΓ ZΘ§
Φ¥Κ· ΐΒΡΕ‘≥Τ÷––ΡΈΣΘ®$\frac{kΠ–}{2}$+$\frac{Π–}{6}$Θ§0Θ©Θ§kΓ ZΘ°
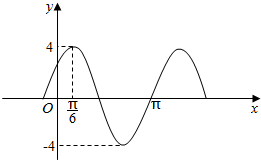
Θ®2Θ©»τΫΪfΘ®xΘ©œρΉσΤΫ“Τ$\frac{Π–}{4}$ΗωΒΞΈΜΒΟΒΫΚ· ΐgΘ®xΘ©=fΘ®x+$\frac{Π–}{4}$Θ©=2sin[2Θ®x+$\frac{Π–}{4}$Θ©-$\frac{Π–}{3}$]+1=2sinΘ®2x+$\frac{Π–}{6}$Θ©+1Θ§
…ηgΘ®xΘ©…œΒψΘ®x1Θ§y1Θ©ΙΊ”Ύ÷±œΏy=2Ε‘≥ΤΒΡΒψΒΡΉχ±ξΈΣΘ®xΘ§yΘ©Θ§
‘ρ$\left\{\begin{array}{l}{{x}_{1}=x}\\{\frac{{y}_{1}+y}{2}=2}\end{array}\right.$Θ§Φ¥$\left\{\begin{array}{l}{{x}_{1}=x}\\{{y}_{1}=4-y}\end{array}\right.$Θ§¥ζ»κgΘ®xΘ©=2sinΘ®2x+$\frac{Π–}{6}$Θ©+1Θ§
ΒΟ4-y=2sinΘ®2x+$\frac{Π–}{6}$Θ©+1Θ§
Φ¥y=3-2sinΘ®2x+$\frac{Π–}{6}$Θ©Θ§
”…2kΠ–+$\frac{Π–}{2}$Γή2x+$\frac{Π–}{6}$Γή2kΠ–+$\frac{3Π–}{2}$Θ§kΓ ZΘ§
ΒΟkΠ–+$\frac{Π–}{6}$ΓήxΓήkΠ–+$\frac{2Π–}{3}$Θ§kΓ ZΘ§
Φ¥Κ· ΐΒΡΒΞΒςΒί‘ω«χΦδΈΣ[kΠ–+$\frac{Π–}{6}$Θ§kΠ–+$\frac{2Π–}{3}$]Θ§kΓ ZΘ°
ΒψΤά ±ΨΧβ÷ς“ΣΩΦ≤ι»ΐΫ«Κ· ΐΒΡΜ·ΦρΚΆ»ΐΫ«Κ· ΐ–‘÷ ΒΡΩΦ≤ιΘ§άϊ”ΟœρΝΩ ΐΝΩΜΐΒΡΙΪ Ϋ“‘ΦΑ»ΐΫ«Κ· ΐΒΡΆΦœσΙΊœΒΘ§«σ≥ωœύ”ΠΒΡΫβΈω Ϋ «ΫβΨω±ΨΧβΒΡΙΊΦϋΘ°


 ΩΣ–ΡΆήΩΎΥψΧβΩ®œΒΝ–¥πΑΗ
ΩΣ–ΡΆήΩΎΥψΧβΩ®œΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | $arctan\frac{3}{4}$ | BΘ° | $Π–-arctan\frac{3}{4}$ | CΘ° | $arctan\frac{4}{3}$ | DΘ° | $Π–-arctan\frac{4}{3}$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | $[{3Θ§\;\;\sqrt{10}}]$ | BΘ° | [3Θ§5] | CΘ° | [3Θ§4] | DΘ° | $[{\sqrt{10}Θ§\;\;5}]$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 2Ηω | BΘ° | 3Ηω | CΘ° | 4Ηω | DΘ° | 5Ηω |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com