
 为锐角,且
为锐角,且 ,函数
,函数 ,数列{
,数列{ }的首项
}的首项 .
. 的表达式;
的表达式; 的前
的前 项和
项和 .
. ;(2)
;(2) .
. ,而已知
,而已知 ,正好符合二倍角公式,所以先利用这个公式求出
,正好符合二倍角公式,所以先利用这个公式求出 ,由于
,由于 为锐角,而
为锐角,而 ,所以
,所以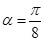 ,将角代入
,将角代入 中,可以求出
中,可以求出 ;第二问,先利用构造法构造一个等比数列
;第二问,先利用构造法构造一个等比数列 ,利用等比数列的通项公式,求出
,利用等比数列的通项公式,求出 ,再求
,再求 ,要求
,要求 ,先把
,先把 分开用2部分表示,一部分符合错位相减法,另一部分是等差数列,最后把这2部分的和加在一起即可.
分开用2部分表示,一部分符合错位相减法,另一部分是等差数列,最后把这2部分的和加在一起即可.
 为锐角,
为锐角, ∴
∴
 5分
5分 , ∴
, ∴
 ∴数列
∴数列 是以2为首项,2为公比的等比数列。
是以2为首项,2为公比的等比数列。 ,∴
,∴ , 9分
, 9分
 的前
的前 项和
项和




 12分
12分

科目:高中数学 来源:不详 题型:解答题
 上的值域;
上的值域; 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
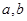 ,函数
,函数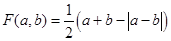 .如果函数
.如果函数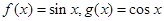 ,那么对于函数
,那么对于函数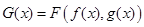 .对于下列五种说法:
.对于下列五种说法: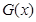 的值域是
的值域是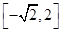 ;
;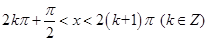 时,
时,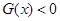 ;
;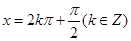 时,该函数取最大值1;
时,该函数取最大值1;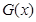 图象在
图象在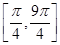 上相邻两个最高点的距离是相邻两个最低点的距离的4倍;
上相邻两个最高点的距离是相邻两个最低点的距离的4倍;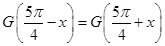 恒成立.
恒成立.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com