
【题目】在四棱锥![]() 中,底面
中,底面![]() 是正方形,顶点
是正方形,顶点![]() 在底面的射影是底面的中心,且各顶点都在同一球面上,若该四棱锥的侧棱长为
在底面的射影是底面的中心,且各顶点都在同一球面上,若该四棱锥的侧棱长为![]() ,体积为4,且四棱锥的高为整数,则此球的半径等于(参考公式:
,体积为4,且四棱锥的高为整数,则此球的半径等于(参考公式:![]() )( )
)( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(Ⅰ)若函数![]() 的图象在
的图象在![]() 处的切线为
处的切线为![]() ,当实数
,当实数![]() 变化时,求证:直线
变化时,求证:直线![]() 经过定点;
经过定点;
(Ⅱ)若函数![]() 有两个极值点,求实数
有两个极值点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
, ![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学只有两位说的话是对的,则获得一等奖的作品是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,焦点在坐标轴上,且经过
的中心在原点,焦点在坐标轴上,且经过![]() ,
,![]() .
.
(Ⅰ)求椭圆的标准方程和离心率;
(Ⅱ)四边形![]() 的四个顶点都在椭圆
的四个顶点都在椭圆![]() 上,且对角线
上,且对角线![]() ,
,![]() 过原点
过原点![]() ,若
,若![]() ,求证:四边形
,求证:四边形![]() 的面积为定值,并求出此定值.
的面积为定值,并求出此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() ,离心率为
,离心率为![]() .
.
(![]() )求椭圆
)求椭圆![]() 的方程.
的方程.
(![]() )直线
)直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 是椭圆
是椭圆![]() 的右顶点.直线
的右顶点.直线![]() 与直线
与直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
,![]() 两点,试问在
两点,试问在![]() 轴上是否存在一个定点
轴上是否存在一个定点![]() 使得
使得![]() ?若是,求出定点
?若是,求出定点![]() 坐标;若不是,说明理由.
坐标;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
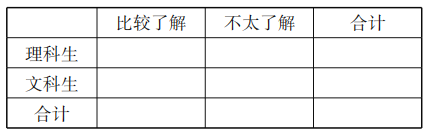
【题目】阿基米德是古希腊伟大的哲学家、数学家、物理学家,对几何学、力学等学科作出过卓越贡献.为调查中学生对这一伟大科学家的了解程度,某调查小组随机抽取了某市的100名高中生,请他们列举阿基米德的成就,把能列举阿基米德成就不少于3项的称为“比较了解”,少于三项的称为“不太了解”他们的调查结果如下:

(1)完成如下![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为,了解阿基米德与选择文理科有关?
的把握认为,了解阿基米德与选择文理科有关?
(2)在抽取的100名高中生中,按照文理科采用分层抽样的方法抽取10人的样本.
(ⅰ)求抽取的文科生和理科生的人数;
(ⅱ)从10人的样本中随机抽取两人,求两人都是文科生的概率.
参考数据:

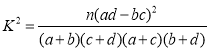 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016高考新课标II,理15)有三张卡片,分别写有1和2,1和3,2和3.甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以原点
为参数).在以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】噪声污染已经成为影响人们身体健康和生活质量的严重问题,为了了解声音强度![]() (单位:分贝)与声音能量
(单位:分贝)与声音能量![]() (单位:
(单位:![]() )之间的关系,将测量得到的声音强度
)之间的关系,将测量得到的声音强度![]() 和声音能量
和声音能量![]() (
(![]() ,2,…,10)数据作了初步处理,得到如图散点图及一些统计量的值.
,2,…,10)数据作了初步处理,得到如图散点图及一些统计量的值.

表中![]() ,
,![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为声音强度
哪一个适宜作为声音强度![]() 关于声音能量
关于声音能量![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据表中数据,求声音强度![]() 关于声音能量
关于声音能量![]() 的回归方程;
的回归方程;
(3)当声音强度大于60分贝时属于噪音,会产生噪音污染,城市中某点![]() 共受到两个声源的影响,这两个声源的声音能量分别是
共受到两个声源的影响,这两个声源的声音能量分别是![]() 和
和![]() ,且
,且![]() .已知点
.已知点![]() 的声音能量等于声音能量
的声音能量等于声音能量![]() 与
与![]() 之和.请根据(1)中的回归方程,判断
之和.请根据(1)中的回归方程,判断![]() 点是否受到噪音污染的干扰,并说明理由.
点是否受到噪音污染的干扰,并说明理由.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
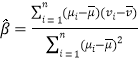 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com