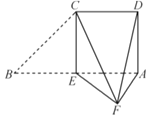
【题目】如图，在直角梯形ABCD中，
，
，
，E为AB的中点
将
沿CE折起，使点B到达点F的位置，且平面CEF与平面ADCE所成的二面角为
．
求证：平面
平面AEF；
求直线DF与平面CEF所成角的正弦值．
寒假乐园北京教育出版社系列答案科目：高中数学 来源： 题型：
【题目】如图，在△MBC中，MA是BC边上的高，MA＝3，AC＝4，将△MBC沿MA进行翻折，使得∠BAC＝90°如图，再过点B作BD∥AC，连接AD，CD，MD且
，∠CAD＝30°．
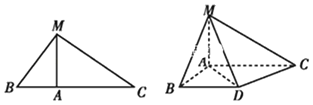
（1）求证：平面MCD⊥平面MAD；
（2）求点B到平面MAD的距离．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的焦距为
，且过点
．
（1）求椭圆的方程；
（2）已知
，是否存在
使得点
关于
的对称点
（不同于点）在椭圆
上？若存在求出此时直线的方程，若不存在说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】进入21世纪，互联网和通讯技术高速发展使商务进入一个全新的阶段，网上购物这一方便、快捷的购物形式已经被越来越多的人所接受
某互联网公司为进一步了解大学生的网上购物的情况，对大学生的消费金额进行了调查研究，得到如下统计表：
组数 | 消费金额 | 人数 | 频率 |
第一组 |
| 1100 |
|
第二组 |
| 3900 |
|
第三组 |
| 3000 | p |
第四组 |
| 1200 |
|
第五组 | 不低于200元 | m |
|
求m，p的值；
该公司从参与调查且购物满150元的学生中采用分层抽样的方法抽取
作为中奖用户，再随机抽取中奖用户的
获得一等奖求第五组至少1人获得一等奖的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】以下说法错误的是（ ）
A.复数
满足
，则复数在复平面上对应的点的轨迹为直线.
B.
为
上连续可导的函数，若
，则
为极值点.
C.若
，
，
，则
.
D.
为抛物线
的两点，
为坐标原点，若
，则直线
过定点
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，椭圆
经过点
，且点
到椭圆的两焦点的距离之和为
.
（l）求椭圆
的标准方程；
（2）若
是椭圆上的两个点，线段
的中垂线
的斜率为
且直线与交于点
，
为坐标原点，求证：
三点共线．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了解某品种一批树苗生长情况，在该批树苗中随机抽取了容量为
的样本，测量树苗高度（单位：
），经统计，其高度均在区间
内，将其按
，
，
，
，
，
分成
组，制成如图所示的频率分布直方图．其中高度为27cm及以上的树苗为优质树苗．
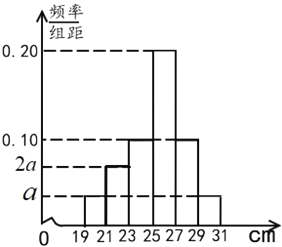
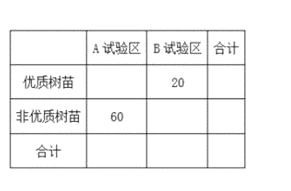
（1）求图中
的值；
（2）已知所抽取这棵树苗来自于
两个试验区，部分数据如下列联表：将列联表补充完整，并判断是否有
的把握认为优质树苗与两个试验区有关系，并说明理由；
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式：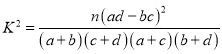
，其中
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某市为了了解民众对开展创建文明城市工作以来的满意度，随机调查了40名群众，并将他们随机分成
，
两组，每组20人，组群众给第一阶段的创文工作评分，组群众给第二阶段的创文工作评分，根据两组群众的评分绘制了如图所示的茎叶图.
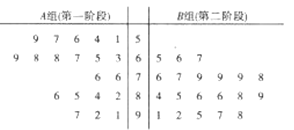
（Ⅰ）根据茎叶图比较群众对两个阶段的创文工作满意度评分的平均值和集中程度（不要求计算出具体值，给出结论即可）；
（Ⅱ）完成下面的列联表，并通过计算判断是否有
的把握认为民众对两个阶段创文工作的满意度存在差异？
低于70分 | 不低于70分 | 合计 | |
第一阶段 | |||
第二阶段 | |||
合计 |
参考公式：
，
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
