
【题目】如图1,在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图2,连结
,如图2,连结![]() ,
, ![]() .
.
(Ⅰ)求证:平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 为
为![]() 中点,求直线
中点,求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)线段![]() 上是否存在一点
上是否存在一点![]() ,使二面角
,使二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

【答案】(Ⅰ)见解析(Ⅱ)![]() (Ⅲ)
(Ⅲ)![]()
【解析】试题分析:(Ⅰ)因为![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 中点,所以
中点,所以![]() //
// ![]() .因为
.因为![]() ,所以
,所以![]() .所以
.所以![]() .因为
.因为![]() ,所以
,所以![]() .又因为
.又因为![]()
![]() =
= ![]() ,所以
,所以![]()
![]() 平面
平面![]() ,由此可以证明平面
,由此可以证明平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)因为![]() ,
, ![]() ,
, ![]() ,所以
,所以![]() ,
, ![]() ,
, ![]() 两两互相垂直.以
两两互相垂直.以![]() 为坐标原点,建立如图所示的空间直角坐标系
为坐标原点,建立如图所示的空间直角坐标系![]() ,得出平面
,得出平面![]() 的一个法向量
的一个法向量![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则![]() ,即得解.
,即得解.
(Ⅲ)假设线段![]() 上存在一点
上存在一点![]() ,使二面角
,使二面角![]() 的余弦值为
的余弦值为![]() .设
.设![]() ,
, ![]() ,得出
,得出![]() ,
, ![]() ,
, ![]() .易得平面
.易得平面![]() 的一个法向量为
的一个法向量为![]() ,求出平面
,求出平面![]() 的一个法向量
的一个法向量![]() ,则有
,则有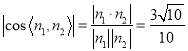 ,即
,即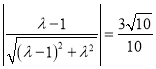 ,解得
,解得![]() 的值,即得解.
的值,即得解.
试题解析:
(Ⅰ)证:因为![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 中点,所以
中点,所以![]() //
// ![]() .
.
因为![]() ,所以
,所以![]() .所以
.所以![]() .
.
因为![]() ,所以
,所以![]() .
.
又因为![]()
![]() =
= ![]() ,所以
,所以![]()
![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,所以平面
,所以平面![]()
![]() 平面
平面![]() .
.
(Ⅱ)解: 因为![]() ,
, ![]() ,
, ![]() ,所以
,所以![]() ,
, ![]() ,
, ![]() 两两互相垂直.
两两互相垂直.
以![]() 为坐标原点,建立如图所示的空间直角坐标系
为坐标原点,建立如图所示的空间直角坐标系![]() ,
,
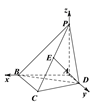
依题意有![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
设平面![]() 的一个法向量
的一个法向量![]() ,
,
则有![]() 即
即![]() 令
令![]() 得
得![]() ,
, ![]() .所以
.所以![]() .
.
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则![]() .
.
故直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(Ⅲ)解:假设线段![]() 上存在一点
上存在一点![]() ,使二面角
,使二面角![]() 的余弦值为
的余弦值为![]() .
.
设![]() ,
, ![]() ,则
,则![]() ,即
,即![]() .
.
所以![]() ,
, ![]() ,
, ![]() .
.
易得平面![]() 的一个法向量为
的一个法向量为![]() .
.
设平面![]() 的一个法向量
的一个法向量![]() ,
,
则有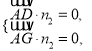 即
即![]() 令
令![]() ,则
,则![]() .
.
若二面角![]() 的余弦值为
的余弦值为![]() ,
,
则有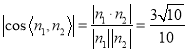 ,即img src="http://thumb.zyjl.cn/questionBank/Upload/2018/09/23/10/f3ee7bee/SYS201809231026007410293450_DA/SYS201809231026007410293450_DA.133.png" width="156" height="69" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,
,即img src="http://thumb.zyjl.cn/questionBank/Upload/2018/09/23/10/f3ee7bee/SYS201809231026007410293450_DA/SYS201809231026007410293450_DA.133.png" width="156" height="69" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,
解得, ![]() ,
, ![]() .又因为
.又因为![]() ,所以
,所以![]() .
.
故线段![]() 上存在一点
上存在一点![]() ,使二面角
,使二面角![]() 的余弦值为
的余弦值为![]() ,且
,且![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥PABCD中,AD⊥平面PDC,AD∥BC,PD⊥PB,AD=1,BC=3,CD=4,PD=2.

(1)求异面直线AP与BC所成角的余弦值;
(2)求证:PD⊥平面PBC;
(3)求直线AB与平面PBC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P﹣ABCD中,PD⊥底面ABCD,AD∥BC,AC⊥DB,∠CAD=60°,AD=2,PD=1.
(1)证明:AC⊥BP;
(2)求二面角C﹣AP﹣D的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高三年级期中考试的学生中随机统计了40名学生的政治成绩,这40名学生的成绩全部在40分至100分之间,据此绘制了如图所示的样本频率分布直方图.

(1)求成绩在[80,90)的学生人数;
(2)从成绩大于等于80分的学生中随机选2名学生,求至少有1 名学生成绩在[90,100]的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:
①对立事件一定是互斥事件;②若A,B为两个随机事件,则P(A∪B)=P(A)+P(B);③若事件A,B,C彼此互斥,则P(A)+P(B)+P(C)=1;④若事件A,B满足P(A)+P(B)=1,则A与B是对立事件.
其中正确命题的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将号码分别为1、2、…、9的九个小球放入一个袋中,这些小球仅号码不同,其余完全相同,甲从袋中摸出一个球.其号码为a,放回后,乙从此袋中再摸出一个球,其号码为b,则使不等式a-2b+10>0成立的事件发生的概率等于________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列说法:
①在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适;
②用相关指数R2来刻画回归的效果,R2值越大,说明模型的拟合效果越好;
③比较两个模型的拟合效果,可以比较残差平方和的大小,残差平方和越小的模型,拟合效果越好.
④在研究气温和热茶销售杯数的关系时,若求得相关指数R2≈0.85,则表明气温解释了15%的热茶销售杯数变化.
其中正确命题的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1= ![]() ,an+1an=2an+1﹣1(n∈N*),令bn=an﹣1.
,an+1an=2an+1﹣1(n∈N*),令bn=an﹣1.
(1)求数列{bn}的通项公式;
(2)令cn= ![]() ,求证:c1+c2+…+cn<n+
,求证:c1+c2+…+cn<n+ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin(ωx+φ)+1(![]() )的最小正周期为π,且
)的最小正周期为π,且![]() .
.
(1)求ω和φ的值;
(2)函数f(x)的图象纵坐标不变的情况下向右平移![]() 个单位,得到函数g(x)的图象,
个单位,得到函数g(x)的图象,
①求函数g(x)的单调增区间;
②求函数g(x)在![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com