
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程
的参数方程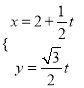 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为:
的极坐标方程为: ![]() .
.
(1)把直线![]() 的参数方程化为极坐标方程,把曲线
的参数方程化为极坐标方程,把曲线![]() 的极坐标方程化为普通方程;
的极坐标方程化为普通方程;
(2)求直线![]() 与曲线
与曲线![]() 交点的极坐标(
交点的极坐标(![]() ≥0,0≤
≥0,0≤![]() ).
).
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】如图,已知平面QBC与直线PA均垂直于Rt△ABC所在平面,且PA=AB=AC.
(1)求证:PA∥平面QBC;
(2)PQ⊥平面QBC,求二面角Q﹣PB﹣A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣2)2+y2=9,直线l:x+y=0.
(1)求过圆C的圆心且与直线l垂直的直线n的方程;
(2)求与圆C相切,且与直线l平行的直线m的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】水培植物需要一种植物专用营养液,已知每投放![]() (
(![]() 且
且![]() )个单位的营养液,它在水中释放的浓度
)个单位的营养液,它在水中释放的浓度![]() (克/升)随着时间
(克/升)随着时间![]() (天)变化的函数关系式近似为
(天)变化的函数关系式近似为![]() ,其中
,其中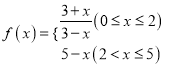 ,若多次投放,则某一时刻水中的营养液浓度为每次投放的营养液在相应时刻所释放的浓度之和,根据经验,当水中营养液的浓度不低于4(克/升)时,它才能有效.
,若多次投放,则某一时刻水中的营养液浓度为每次投放的营养液在相应时刻所释放的浓度之和,根据经验,当水中营养液的浓度不低于4(克/升)时,它才能有效.
(1)若只投放一次2个单位的营养液,则有效时间最多可能达到几天?
(2)若先投放2个单位的营养液,3天后再投放![]() 个单位的营养液,要使接下来的2天中,营养液能够持续有效,试求
个单位的营养液,要使接下来的2天中,营养液能够持续有效,试求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:①函数f(x)=sin2x一cos2x的最小正周期是![]() ;
;
②在等比数列〔![]() }中,若
}中,若![]() ,则a3=士2;
,则a3=士2;
③设函数f(x)=![]() ,若
,若![]() 有意义,则
有意义,则![]()
④平面四边形ABCD中, ![]() ,则四边形ABCD是
,则四边形ABCD是
菱形. 其中所有的真命题是:( )
A. ①②④ B. ①④ C. ③④ D. ①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ,则导函数f′(x)是( )
,则导函数f′(x)是( )
A.仅有最小值的奇函数
B.既有最大值,又有最小值的偶函数
C.仅有最大值的偶函数
D.既有最大值,又有最小值的奇函数
查看答案和解析>>
科目:高中数学 来源: 题型:
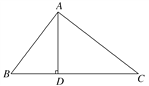
【题目】如图,在△ABC中,AD⊥BC于D,下列条件:
①∠B+∠DAC=90°,
②∠B=∠DAC,
③![]() ,
,
④AB2=BD·BC.
其中一定能够判定△ABC是直角三角形的共有( )
A. 3个 B. 2个 C. 1个 D. 0个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com