
【题目】已知f(x)是定义在[-1,1]上的奇函数,且f(1)=1,若任意的a、b∈[-1,1],当a+b≠0时,总有![]() .
.
(1)判断函数f(x)在[-1,1]上的单调性,并证明你的结论;
(2)解不等式:![]() ;
;
(3)若f(x)≤m2-2pm+1对所有的x∈[-1,1]恒成立,其中p∈[-1,1](p是常数),试用常数p表示实数m的取值范围.
科目:高中数学 来源: 题型:
【题目】某大学进行自主招生时,需要进行逻辑思维和阅读表达两项能力的测试.学校对参加测试的200名学生的逻辑思维成绩、阅读表达成绩以及这两项的总成绩进行了排名.其中甲、乙、丙三位同学的排名情况如下图所示:
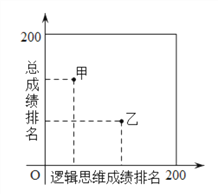

得出下面四个结论:
①甲同学的阅读表达成绩排名比他的逻辑思维成绩排名更靠前
②乙同学的逻辑思维成绩排名比他的阅读表达成绩排名更靠前
③甲、乙、丙三位同学的逻辑思维成绩排名中,甲同学更靠前
④乙同学的总成绩排名比丙同学的总成绩排名更靠前
则所有正确结论的序号是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在直角梯形ABCD中,AB∥CD,∠DAB=90°,点E、F分别在CD、AB上,且EF⊥CD,BE⊥BC,BC=1,CE=2.现将矩形ADEF沿EF折起,使平面ADEF与平面EFBC垂直(如图2). 
(1)求证:CD∥面ABF;
(2)当AF的长为何值时,二面角A﹣BC﹣F的大小为30°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣1|+|x+a|,其中a为实常数.
(1)若函数f(x)的最小值为2,求a的值;
(2)当x∈[0,1]时,不等式|x﹣2|≥f(x)恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M过A(-4,0),B(1,5),C(6,0)三点.
(Ⅰ)求圆M的方程
(Ⅱ)若直线ax-y+5=0(a>0)与圆M相交于P,Q两点,是否存在实数a,使得弦PQ的垂直平分线l过点E(-2,4),若存在,求出实数a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】端午节吃粽子是我国的传统习俗,设一盘中装有![]() 个粽子,其中豆沙粽
个粽子,其中豆沙粽![]() 个,肉粽
个,肉粽![]() 个,白粽
个,白粽![]() 个,这三种粽子的外观完全相同,从中任意选取
个,这三种粽子的外观完全相同,从中任意选取![]() 个.
个.
(![]() )求三种粽子各取到
)求三种粽子各取到![]() 个的概率.
个的概率.
(![]() )设
)设![]() 表示取到的豆沙粽个数,求
表示取到的豆沙粽个数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos2x﹣sin2xsinφ﹣2cos2xsin2 ![]() (0<φ<
(0<φ< ![]() )的图象的一个对称中心为(
)的图象的一个对称中心为( ![]() ,0),则下列说法不正确的是( )
,0),则下列说法不正确的是( )
A.直线x= ![]() π是函数f(x)的图象的一条对称轴
π是函数f(x)的图象的一条对称轴
B.函数f(x)在[0, ![]() ]上单调递减
]上单调递减
C.函数f(x)的图象向右平移 ![]() 个单位可得到y=cos2x的图象
个单位可得到y=cos2x的图象
D.函数f(x)在x∈[0, ![]() ]上的最小值为﹣1
]上的最小值为﹣1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com