
【题目】某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:min)进行调查,将收集到的数据分成[0,10),[10,20),[20,30),[30,40),[40,50),[50,60]六组,并作出频率分布直方图(如图).将日均课外体育锻炼时间不低于40 min的学生评价为“课外体育达标”.

(1)请根据频率分布直方图中的数据填写下面的2×2列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?
课外体育不达标 | 课外体育达标 | 总计 | |
男 | 60 |
|
|
女 |
|
| 110 |
总计 |
|
|
|
(2)现从“课外体育达标”学生中按分层抽样抽取5人,再从这5名学生中随机抽取2人参加体育知识问卷调查,求抽取的这2人课外体育锻炼时间都在[40,50)内的概率.
附参考公式与数据:K2=![]()
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
【答案】(1)答案见解析;(2)0.6.
【解析】试题分析:
(1)根据频率分布直方图,得“课外体育达标”的学生数为50.由2×2列联表可知“课外体育达标”的男生人数为30,女生人数为20.据此完成列联表即可,计算观测值K2≈6.061<6.635,故在犯错误的概率不超过0.01的前提下不能认为“课外体育达标”与性别有关.
(2)从“课外体育达标”学生中按分层抽样抽取5人,其中课外体育锻炼时间在[40,50)内有4人,列出所有可能的基本事件,共有10种,其中2人都在[40,50)内的基本事件有6种,故所求的概率为![]() =0.6.
=0.6.
试题解析:
(1)根据频率分布直方图,得“课外体育达标”的学生数为200×(0.020+0.005)×10=50.
由2×2列联表可知“课外体育达标”的男生人数为30,女生人数为20.
补全2×2列联表如下:
课外体育不达标 | 课外体育达标 | 总计 | |
男 | 60 | 30 | 90 |
女 | 90 | 20 | 110 |
总计 | 150 | 50 | 200 |
计算K2=![]() ≈6.061<6.635,故在犯错误的概率不超过0.01的前提下不能认为“课外体育达标”与性别有关.
≈6.061<6.635,故在犯错误的概率不超过0.01的前提下不能认为“课外体育达标”与性别有关.
(2)从“课外体育达标”学生中按分层抽样抽取5人,其中课外体育锻炼时间在[40,50)内有5×![]() =4(人),分别记为a,b,c,d;
=4(人),分别记为a,b,c,d;
在[50,60]上有1人,记为E.
从这5人中抽取2人,总的基本事件有ab,ac,ad,aE,bc,bd,bE,cd,cE,dE共10种,其中2人都在[40,50)内的基本事件有ab,ac,ad,bc,bd,cd共6种,故所求的概率为![]() =0.6.
=0.6.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:高中数学 来源: 题型:
【题目】随着互联网技术的快速发展,人们更加关注如何高效地获取有价值的信息,网络知识付费近两年呈现出爆发式的增长,为了了解网民对网络知识付费的态度,某网站随机抽查了![]() 岁及以上不足
岁及以上不足![]() 岁的网民共
岁的网民共![]() 人,调查结果如下:
人,调查结果如下:

(1)请完成上面的![]() 列联表,并判断在犯错误的概率不超过
列联表,并判断在犯错误的概率不超过![]() 的前提下,能否认为网民对网络知识付费的态度与年龄有关?
的前提下,能否认为网民对网络知识付费的态度与年龄有关?
(2)在上述样本中用分层抽样的方法,从支持和反对网络知识付费的两组网民中抽取![]() 名,若在上述
名,若在上述![]() 名网民中随机选
名网民中随机选![]() 人,设这
人,设这![]() 人中反对态度的人数为随机变量
人中反对态度的人数为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:  ,
, ![]() .
.
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲同学写出三个不等式:![]() :
:![]() ,
,![]() :
:![]() ,
,![]() :
:![]() ,然后将
,然后将![]() 的值告诉了乙、丙、丁三位同学,要求他们各用一句话来描述,以下是甲、乙、丙、丁四位同学的描述:
的值告诉了乙、丙、丁三位同学,要求他们各用一句话来描述,以下是甲、乙、丙、丁四位同学的描述:
乙:![]() 为整数;
为整数;
丙:![]() 是
是![]() 成立的充分不必要条件;
成立的充分不必要条件;
丁:![]() 是
是![]() 成立的必要不充分条件;
成立的必要不充分条件;
甲:三位同学说得都对,则![]() 的值为__________.
的值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:
年 份 | 2013 | 2014 | 2015 | 2016 | 2017 |
时间代号t | 1 | 2 | 3 | 4 | 5 |
储蓄存款y/千亿元 | 5 | 6 | 7 | 8 | 10 |
(1)求y关于t的线性回归方程![]() t+
t+![]() ;
;
(2)用所求回归方程预测该地区2018年(t=6)的人民币储蓄存款.
附:回归方程![]() t+
t+![]() 中,
中, .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列问题中,最适合用简单随机抽样方法抽样的是( )
A.某县从该县中、小学生中抽取200人调查他们的视力情况
B.从15种疫苗中抽取5种检测是否合格
C.某大学共有学生5600人,其中专科生有1300人、本科生3000人、研究生1300人,现抽取样本量为280的样本调查学生利用因特网查找学习资料的情况,
D.某学校兴趣小组为了了解移动支付在大众中的熟知度,要对![]() 岁的人群进行随机抽样调查
岁的人群进行随机抽样调查
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】水葫芦原产于巴西,![]() 年作为观赏植物引入中国. 现在南方一些水域水葫芦已泛滥成灾严重影响航道安全和水生动物生长. 某科研团队在某水域放入一定量水葫芦进行研究,发现其蔓延速度越来越快,经过
年作为观赏植物引入中国. 现在南方一些水域水葫芦已泛滥成灾严重影响航道安全和水生动物生长. 某科研团队在某水域放入一定量水葫芦进行研究,发现其蔓延速度越来越快,经过![]() 个月其覆盖面积为
个月其覆盖面积为![]() ,经过
,经过![]() 个月其覆盖面积为
个月其覆盖面积为![]() . 现水葫芦覆盖面积
. 现水葫芦覆盖面积![]() (单位
(单位![]() )与经过时间
)与经过时间![]() 个月的关系有两个函数模型
个月的关系有两个函数模型![]() 与
与![]() 可供选择.
可供选择.
(参考数据:![]() )
)
(Ⅰ)试判断哪个函数模型更合适,并求出该模型的解析式;
(Ⅱ)求原先投放的水葫芦的面积并求约经过几个月该水域中水葫芦面积是当初投放的![]() 倍.
倍.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次高中学科知识竞赛中,对4000名考生的参赛成绩进行统计,可得到如图所示的频率分布直方图,其中分组的区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,60分以下视为不及格,若同一组中数据用该组区间中间值作代表值,则下列说法中正确的是( )
,60分以下视为不及格,若同一组中数据用该组区间中间值作代表值,则下列说法中正确的是( )
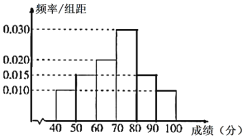
A.成绩在![]() 的考生人数最多B.不及格的考生人数为1000
的考生人数最多B.不及格的考生人数为1000
C.考生竞赛成绩的平均分约为70D.考生竞赛成绩的中位数为75分
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com