
 如图所示,在△OAB中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,点M是AB的靠近B的一个三等分点,点N是OA的靠近A的一个四等分点,若OM与BN相交于点P,求$\overrightarrow{OP}$.
如图所示,在△OAB中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}=\overrightarrow{b}$,点M是AB的靠近B的一个三等分点,点N是OA的靠近A的一个四等分点,若OM与BN相交于点P,求$\overrightarrow{OP}$. 分析 可连接AP,由B,P,N三点共线便可得到$\overrightarrow{BP}=λ\overrightarrow{BN}$,从而得到$\overrightarrow{AP}=(1-λ)\overrightarrow{AB}+\frac{λ}{4}\overrightarrow{AO}$,而同理由O,P,M三点共线可以得到$\overrightarrow{AP}=(1-μ)\overrightarrow{AO}+\frac{2μ}{3}\overrightarrow{AB}$,这样根据平面向量基本定理即可建立关于λ,μ的方程组,可解出λ,μ.从而可表示出$\overrightarrow{AP}$,而由$\overrightarrow{OP}=\overrightarrow{AP}-\overrightarrow{AO}$便可用$\overrightarrow{a},\overrightarrow{b}$表示出$\overrightarrow{OP}$.
解答 解:如图,连接AP;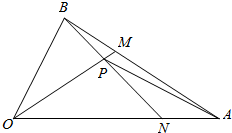
B,P,N三点共线;
∴$\overrightarrow{BP}=λ\overrightarrow{BN}$;
∴$\overrightarrow{AP}-\overrightarrow{AB}=λ(\overrightarrow{AN}-\overrightarrow{AB})$;
∴$\overrightarrow{AP}=(1-λ)\overrightarrow{AB}+\frac{λ}{4}\overrightarrow{AO}$①;
同理,由O,P,M三点共线得,$\overrightarrow{AP}=(1-μ)\overrightarrow{AO}+\frac{2μ}{3}\overrightarrow{AB}$②;
由①②得,$\left\{\begin{array}{l}{1-λ=\frac{2μ}{3}}\\{\frac{λ}{4}=1-μ}\end{array}\right.$;
解得$\left\{\begin{array}{l}{λ=\frac{2}{5}}\\{μ=\frac{9}{10}}\end{array}\right.$;
∴$\overrightarrow{AP}=\frac{3}{5}\overrightarrow{AB}+\frac{1}{10}\overrightarrow{AO}$;
∴$\overrightarrow{OP}=\overrightarrow{AP}-\overrightarrow{AO}=\frac{3}{5}\overrightarrow{AB}-\frac{9}{10}\overrightarrow{AO}$=$\frac{3}{5}(\overrightarrow{OB}-\overrightarrow{OA})+\frac{9}{10}\overrightarrow{OA}=\frac{3}{10}\overrightarrow{OA}$$+\frac{3}{5}\overrightarrow{OB}$=$\frac{3}{10}\overrightarrow{a}+\frac{3}{5}\overrightarrow{b}$.
点评 考查共线向量基本定理,向量减法的几何意义,以及向量的数乘运算,平面向量基本定理.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 如图所示,在正方体ABCD-A1B1C1D1中,E在A1D1上,且$\overrightarrow{{A}_{1}E}=2\overrightarrow{E{D}_{1}}$,F在对角线A1C上,且$\overrightarrow{{A}_{1}F}=\frac{2}{3}\overrightarrow{FC}$.求证:E,F,B三点共线.
如图所示,在正方体ABCD-A1B1C1D1中,E在A1D1上,且$\overrightarrow{{A}_{1}E}=2\overrightarrow{E{D}_{1}}$,F在对角线A1C上,且$\overrightarrow{{A}_{1}F}=\frac{2}{3}\overrightarrow{FC}$.求证:E,F,B三点共线.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com