
【题目】已知定义域为(0,+∞)的函数f(x)满足:
①x>1时,f(x)<0;
②f( ![]() )=1;
)=1;
③对任意的正实数x,y,都有f(xy)=f(x)+f(y).
(1)求证:f( ![]() )=﹣f(x);
)=﹣f(x);
(2)求证:f(x)在定义域内为减函数;
(3)求满足不等式f(log0.5m+3)+f(2log0.5m﹣1)≥﹣2的m集合.
【答案】
(1)证明:令 ![]() ,
, ![]() ,得f(1)=0,
,得f(1)=0,
令 ![]() ,
, ![]() ,得
,得 ![]()
(2)证明:设x1>x2>0,f(x1)﹣f(x2)= ![]() =
= ![]() ,
,
∵x1>x2,∴ ![]() ,∴
,∴ ![]() ,即f(x1)﹣f(x2)<0,
,即f(x1)﹣f(x2)<0,
∴f(x1)<f(x)2,
∴f(x)在(0,+∞)上为减函数
(3)解:∵ ![]() ,∴
,∴ ![]() .
.
f(log0.5m+3)+f(2log0.5m﹣1)≥﹣2,f(log0.5m+3)+f(2log0.5m﹣1)≥f(4),即f[(log0.5m+3)(2log0.5m﹣1)]≥f(4),
∵f(x)定义域上是减函数(log0.5m+3)(2log0.5m﹣1)≤4,
∴ 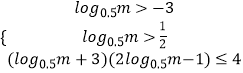
∴ ![]() ,
,
不等式的解集 ![]()
【解析】赋特殊值,令x=y=1,即可求得f(1)=0,令y = ![]() ,即可证得
,即可证得![]() ,(2)利用函数的单调性的定义,设值作差即可,(3)根据题意可求得f(4)=-2,从而可得f(5-x)≥f(2),再利用f(x)在定义域内为减函数,即可求得其解集.
,(2)利用函数的单调性的定义,设值作差即可,(3)根据题意可求得f(4)=-2,从而可得f(5-x)≥f(2),再利用f(x)在定义域内为减函数,即可求得其解集.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,当x∈[0,+∞)时,f(x)=2x﹣2,则不等式f(log2x)>0的解集为( )
A.(0, ![]() )
)
B.( ![]() ,1)∪(2,+∞)
,1)∪(2,+∞)
C.(2,+∞)
D.(0, ![]() )∪(2,+∞)
)∪(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=﹣3x2+a(6﹣a)x+6.
(Ⅰ)解关于a的不等式f(1)>0;
(Ⅱ)若不等式f(x)>b的解集为(﹣1,3),求实数a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一家公司生产某种品牌服装的年固定成本为10万元,每生产1千件需另投入2.7万元.设该公司一年内生产该品牌服装x千件并全部销售完,每千件的销售收入为R(x)万元,且R(x)=  .
.
(1)求年利润W(万元)关于年产量x(千件)的函数解析式;
(2)当年产量为多少千件时,该公司在这一品牌服装的生产中所获得的年利润最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC﹣A1B1C1中,侧棱AA1⊥平面ABC.若AB=AC=AA1=1,BC= ![]() ,则异面直线A1C与B1C1所成的角为 . .
,则异面直线A1C与B1C1所成的角为 . . 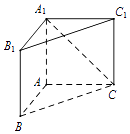
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() (其中常数a>0,且a≠1).
(其中常数a>0,且a≠1).
(1)当a=10时,解关于x的方程f(x)=m(其中常数m>2 ![]() );
);
(2)若函数f(x)在(﹣∞,2]上的最小值是一个与a无关的常数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数fk(x)=2x﹣(k﹣1)2﹣x(k∈Z),x∈R,g(x)= ![]() .
.
(1)若f2(x)=2,求x的值.
(2)判断并证明函数y=g(x)的单调性;
(3)若函数y=f0(2x)+2mf2(x)在x∈[1,+∞)上有零点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知矩形ABCD所在平面垂直于直角梯形ABPE所在平面,平面ABCD∩平面ABPE=AB,且AB=BP=2,AD=AE=1,AE⊥AB,且AE∥BP. (Ⅰ)设点M为棱PD中点,求证:EM∥平面ABCD;
(Ⅱ)线段PD上是否存在一点N,使得直线BN与平面PCD所成角的正弦值等于 ![]() ?若存在,试确定点N的位置;若不存在,请说明理由.
?若存在,试确定点N的位置;若不存在,请说明理由.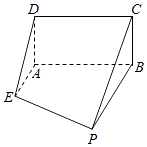
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com