
����Ŀ�����������Ĺ۲��Ԥ�⣺������M�ص�ɳ����һֱ�����Ϸ����ƶ������ƶ��ٶ�v��km/h����ʱ��t��h���ĺ���ͼ����ͼ��ʾ�����߶�OC��һ��T��t��0��������Ĵ���l������OABC��ֱ��l��ಿ�ֵ������Ϊt��h����ɳ������������·��s��km����
��1����t=4ʱ����s��ֵ��
��2����s��t�仯�Ĺ�������ѧ��ϵʽ��ʾ������
��3����N��λ��M�����Ϸ����Ҿ�M��650km�����ж��ⳡɳ�����Ƿ����Ϯ��N�ǣ�����ᣬ��ɳ����������ʱ��������Ϯ��N�ǣ�������ᣬ��˵�����ɣ�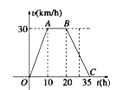
���𰸡��⣺��ֱ��l��v��t�ĺ���ͼ����D�㣬
��1����ͼ��֪����A������Ϊ��10��30������ֱ��OA�Ľ���ʽΪv=3t��
��t=4ʱ��D������Ϊ��4��12����
��OT=4��TD=12��
��S=![]() ��4��12=24��km����
��4��12=24��km����
��2����0��t��10ʱ����ʱOT=t��TD=3t����ͼ1��
��S=![]() t3t=
t3t=![]()
��10��t��20ʱ����ʱOT=t��AD=ET=t��10��TD=30����ͼ2��
��S=S��AOE+S����ADTE=![]() ��10��30+30��t��10��=30t��150��5�֣�
��10��30+30��t��10��=30t��150��5�֣�
��20��t��35ʱ����B��C������ֱ�Ϊ��20��30������35��0��
��ֱ��BC�Ľ���ʽΪv=��2t+70
��D��������t����2t+70��
��TC=35��t��TD=��2t+70����ͼ3��
��S=S����OABC��S��DCT=![]() ��10+35����30��
��10+35����30��![]() ��35��t������2t+70��=����35��t��2+675��
��35��t������2t+70��=����35��t��2+675��
��3���ߵ�t=20ʱ��S=30��20��150=450��km����
��t=35ʱ��S=����35��35��2+675=675��km������450��650��675��
��N�ǻ��ܵ���Ϯ������Ϯʱ��tӦ��20h��35h֮�䣬
�ɩ���35��t��2+675=650�����t=30��t=40���������⣬��ȥ����
����ɳ����������30h������Ϯ��N�ǣ�
����������1����ֱ��l��v��t�ĺ���ͼ����D�㣮��ͼ��֪����A������Ϊ��10��30������ֱ��OA�Ľ���ʽΪv=3t����t=4ʱ��D������Ϊ��4��12����OT=4��TD=12��S=![]() ��4��12=24��km����
��4��12=24��km����
��2���������ۣ���0��t��10ʱ����10��t��20ʱ����20��t��35ʱ��
��3������t��ֵ��Ӧ��S��Ȼ����


 ��������ϵ�д�
��������ϵ�д� ����˼ά����ѵ����ʱ��ѧ��ϵ�д�
����˼ά����ѵ����ʱ��ѧ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������13�֣���֪����![]() ��
��![]() ������
������![]() ��
��
��1����![]() �Ǻ���
�Ǻ���![]() ��һ����ֵ�㣬��
��һ����ֵ�㣬��![]() ��ֵ��
��ֵ��
��2����֤����![]() ʱ��
ʱ��![]() ��
��![]() ������������
������������
��3�����������![]() ���ܴ���
���ܴ���![]() ��ʹ����ʽ
��ʹ����ʽ![]() ����������ʵ��
����������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��.
��.
����������![]() ��
��![]() ��������ƽ����ֱ��
��������ƽ����ֱ��![]() ����ʵ��
����ʵ��![]() ��ֵ��
��ֵ��
��������![]() ��
��![]() �ϵĵ����ԣ�
�ϵĵ����ԣ�
����������![]() ��ʹ��
��ʹ��![]() ��������
��������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���������ĵȲ�����![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ����
����![]() ��
��![]() ��
��
��1��������![]() ��ͨ�ʽ��
��ͨ�ʽ��
��2��������![]() �ǵȲ����У���
�ǵȲ����У���![]() ������㳣��
������㳣��![]() ��ֵ��
��ֵ��
��3����![]() ��
��![]() ����
Ϊ����![]() ��ǰ
��ǰ![]() ��ͣ��Ƿ����������
��ͣ��Ƿ����������![]() ��ʹ��
��ʹ��![]() �������
�������![]() �������������������
�������������������![]() ����Сֵ���������ڣ���˵�����ɣ�
����Сֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=a|x+b|��a��0��a��1��b��R����
��1����f��x��Ϊż��������b��ֵ��
��2����f��x��������[2��+�ޣ�����������������a��bӦ�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�����εIJ˵أ�����ˮƽ���õ�ƽ��ͼ�ε�б����ֱ��ͼ��ֱ�����Σ���ͼ����ABC=45�㣬AB=![]() �� AD=1��DC��BC�������˵ص����Ϊ��
�� AD=1��DC��BC�������˵ص����Ϊ�� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����һ���������ֱ��ͼ������ͼ(��������ͼΪֱ�����Σ�����ͼΪ�����Σ�����ͼΪֱ��������)��
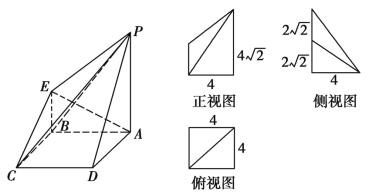
��1��������P-ABCD�������
��2����GΪBC�ϵĶ��㣬��֤��AE��PG��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͼ�У��ı��� ABCD�ǵ������Σ� ![]() ��
�� ![]() ��O��Q�ֱ�Ϊ�߶�AB��CD���е㣬OQ��EF�Ľ���ΪP��OP=1��PQ=2���ֽ�����ABCD��EF����ʹ��
��O��Q�ֱ�Ϊ�߶�AB��CD���е㣬OQ��EF�Ľ���ΪP��OP=1��PQ=2���ֽ�����ABCD��EF����ʹ��![]() ������AD��BC����һ��������ͼ��ʾ��
������AD��BC����һ��������ͼ��ʾ��
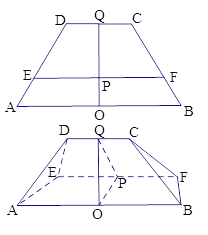
(��)֤����ƽ��ABCD![]() ƽ��ABFE��
ƽ��ABFE��
(��)����ͼ�У� ![]() ��CD=2����ƽ��ADE��ƽ��BCF���������ǵ�����ֵ��
��CD=2����ƽ��ADE��ƽ��BCF���������ǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
��1����![]() ������
������![]() �ϵ�����������ʵ��
�ϵ�����������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2��������Ψһ����![]() ��ʹ��
��ʹ��![]() ��������ʵ��
��������ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com