
【题目】已知函数![]() .
.
(Ⅰ)求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(Ⅱ)求![]() 在
在![]() 上的单调区间;
上的单调区间;
(Ⅲ)当![]() 时,证明:
时,证明:![]() 在
在![]() 上存在最小值.
上存在最小值.
【答案】(Ⅰ)![]() ;(Ⅱ)单调递减区间为
;(Ⅱ)单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ;(Ⅲ)详见解析.
;(Ⅲ)详见解析.
【解析】
(Ⅰ)先求导数,根据导数几何意义得切线斜率,最后根据点斜式得直线方程,(Ⅱ)先求导函数在区间![]() 上零点,列表分析导函数符号变化规律,即得单调区间,(Ⅲ)利用导数研究导函数零点情况,再根据导函数零点确定函数单调性,最后根据单调性确定函数最值.
上零点,列表分析导函数符号变化规律,即得单调区间,(Ⅲ)利用导数研究导函数零点情况,再根据导函数零点确定函数单调性,最后根据单调性确定函数最值.
(Ⅰ)因为![]() ,所以
,所以![]()
则![]() ,
,![]() ,所以切线方程为
,所以切线方程为![]()
(Ⅱ)令![]() ,即
,即![]() ,
,![]() ,得
,得![]()
当![]() 变化时,
变化时,![]() 变化如下:
变化如下:
|
|
|
|
|
| 0 |
|
| 减 | 最小值 | 增 |
所以函数![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]()
(Ⅲ)因为![]() ,所以
,所以![]()
令![]() ,则
,则![]()
因为![]() ,所以
,所以![]()
所以![]() 即
即![]() 在
在![]() 内有唯一解
内有唯一解![]()
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
所以![]() ,又因为
,又因为![]()
所以![]() 在
在![]() 内有唯一零点
内有唯一零点![]()
当![]() 时,
时,![]() 即
即![]() ,
,
当![]() 时,
时,![]() 即
即![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
所以函数![]() 在
在![]() 处取得最小值
处取得最小值
即![]() 时,函数
时,函数![]() 在
在![]() 上存在最小值
上存在最小值


科目:高中数学 来源: 题型:
【题目】如图所示,在长方体![]() 中,点E是棱
中,点E是棱![]() 上的一个动点,若平面
上的一个动点,若平面![]() 交棱
交棱![]() 于点F,给出下列命题:
于点F,给出下列命题:
①四棱锥![]() 的体积恒为定值;
的体积恒为定值;
②对于棱![]() 上任意一点E,在棱
上任意一点E,在棱![]() 上均有相应的点G,使得
上均有相应的点G,使得![]() 平面
平面![]() ;
;
③O为底面![]() 对角线
对角线![]() 和
和![]() 的交点,在棱
的交点,在棱![]() 上存在点H,使
上存在点H,使![]() 平面
平面![]() ;
;
④存在唯一的点E,使得截面四边形![]() 的周长取得最小值.
的周长取得最小值.
其中为真命题的是____________________.(填写所有正确答案的序号)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点![]() ,动点
,动点![]() 在
在![]() 轴上运动,过点
轴上运动,过点![]() 作直线
作直线![]() 交
交![]() 轴于点
轴于点![]() ,延长
,延长![]() 至点
至点![]() ,使
,使![]() .
.![]() 点
点![]() 的轨迹是曲线
的轨迹是曲线![]() .
.

(1)求曲线![]() 的方程;
的方程;
(2)若![]() ,
,![]() 是曲线
是曲线![]() 上的两个动点,满足
上的两个动点,满足![]() ,证明:直线
,证明:直线![]() 过定点;
过定点;
(3)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,
,![]() ,求直线
,求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 经过点
经过点![]() ,离心率为
,离心率为![]() .过原点
.过原点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有两个不同的交点
有两个不同的交点![]() .
.
(1)求椭圆![]() 长半轴长;
长半轴长;
(2)求![]() 最大值;
最大值;
(3)若直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,求证:
,求证:![]() 的面积与
的面积与![]() 的面积的乘积为定值.
的面积的乘积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为降低空气污染,提高环境质量,政府决定对汽车尾气进行整治.某厂家生产甲、乙两种不同型号的汽车尾气净化器,为保证净化器的质量,分别从甲、乙两种型号的净化器中随机抽取100件作为样本进行产品性能质量评估,评估综合得分![]() 都在区间
都在区间![]() .已知评估综合得分与产品等级如下表:
.已知评估综合得分与产品等级如下表:

根据评估综合得分,统计整理得到了甲型号的样本频数分布表和乙型号的样本频率分布直方图(图表如下).


甲型 乙型
(Ⅰ)从厂家生产的乙型净化器中随机抽取一件,估计这件产品为二级品的概率;
(Ⅱ)从厂家生产的乙型净化器中随机抽取3件,设随机变量![]() 为其中二级品的个数,求
为其中二级品的个数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)根据图表数据,请自定标准,对甲、乙两种型号汽车尾气净化器的优劣情况进行比较.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某共享单车经营企业欲向甲市投放单车,为制定适宜的经营策略,该企业首先在已投放单车的乙市进行单车使用情况调查.调查过程分随机问卷、整理分析及开座谈会三个阶段.在随机问卷阶段,A,B两个调查小组分赴全市不同区域发放问卷并及时收回;在整理分析阶段,两个调查小组从所获取的有效问卷中,针对15至45岁的人群,按比例随机抽取了300份,进行了数据统计,具体情况如下表:
组别 年龄 | A组统计结果 | B组统计结果 | ||
经常使用单车 | 偶尔使用单车 | 经常使用单车 | 偶尔使用单车 | |
| 27人 | 13人 | 40人 | 20人 |
| 23人 | 17人 | 35人 | 25人 |
| 20人 | 20人 | 35人 | 25人 |
(1)先用分层抽样的方法从上述300人中按“年龄是否达到35岁”抽出一个容量为60人的样本,再用分层抽样的方法将“年龄达到35岁”的被抽个体数分配到“经常使用单车”和“偶尔使用单车”中去.求这60人中“年龄达到35岁且偶尔使用单车”的人数;
(2)从统计数据可直观得出“是否经常使用共享单车与年龄(记作![]() 岁)有关”的结论.在用独立性检验的方法说明该结论成立时,为使犯错误的概率尽可能小,年龄
岁)有关”的结论.在用独立性检验的方法说明该结论成立时,为使犯错误的概率尽可能小,年龄![]() 应取25还是35?请通过比较
应取25还是35?请通过比较![]() 的观测值的大小加以说明.
的观测值的大小加以说明.
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的准线l经过椭圆
的准线l经过椭圆![]() 的左焦点,且l与椭圆交于A,B两点,过椭圆N右焦点
的左焦点,且l与椭圆交于A,B两点,过椭圆N右焦点![]() 的直线交抛物线M于C,D两点,交椭圆于G,H两点,且
的直线交抛物线M于C,D两点,交椭圆于G,H两点,且![]() 面积为3.
面积为3.
(1)求椭圆N的方程;
(2)当![]() 时,求
时,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校科技小组在计算机上模拟航天器变轨返回试验,设计方案如图:航天器运行(按顺时针方向)的轨迹方程为![]() ,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以
,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以![]() 轴为对称轴、
轴为对称轴、![]() 为顶点的抛物线的实线部分,降落点为
为顶点的抛物线的实线部分,降落点为![]() .观测点
.观测点![]() 、
、![]() 同时跟踪航天器.
同时跟踪航天器.
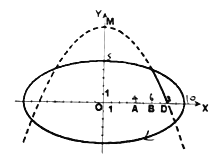
(1)求航天器变轨后的运行轨迹所在的曲线方程;
(2)试问:当航天器在![]() 轴上方时,观测点
轴上方时,观测点![]() 、
、![]() 测得离航天器的距离分别为多少时,应向航天器发出变轨指令?
测得离航天器的距离分别为多少时,应向航天器发出变轨指令?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com