
ЁОЬтФПЁПШєЪ§Са![]() гыКЏЪ§
гыКЏЪ§![]() ТњзуЃКЂй
ТњзуЃКЂй![]() ЕФШЮвтСНЯюОљВЛЯрЕШЃЌЧв
ЕФШЮвтСНЯюОљВЛЯрЕШЃЌЧв![]() ЕФЖЈвхгђЮЊ
ЕФЖЈвхгђЮЊ![]() ЃЛЂкЪ§Са
ЃЛЂкЪ§Са![]() ЕФЧА
ЕФЧА![]() ЕФЯюЕФКЭ
ЕФЯюЕФКЭ![]() ЖдШЮвтЕФ
ЖдШЮвтЕФ![]() ЖМГЩСЂЃЌдђГЦ
ЖМГЩСЂЃЌдђГЦ![]() гы
гы![]() ОпгаЁАЙВЩњЙиЯЕЁБЃЎ
ОпгаЁАЙВЩњЙиЯЕЁБЃЎ
ЃЈ1ЃЉШє![]() ЃЌЪдаДГівЛИігыЪ§Са
ЃЌЪдаДГівЛИігыЪ§Са![]() ОпгаЁАЙВЩњЙиЯЕЁБЕФКЏЪ§
ОпгаЁАЙВЩњЙиЯЕЁБЕФКЏЪ§![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШє![]() гыЪ§Са
гыЪ§Са![]() ОпгаЁАЙВЩњЙиЯЕЁБЃЌЧѓЪЕЪ§Жд
ОпгаЁАЙВЩњЙиЯЕЁБЃЌЧѓЪЕЪ§Жд![]() ЫљЙЙГЩЕФМЏКЯЃЌВЂаДГі
ЫљЙЙГЩЕФМЏКЯЃЌВЂаДГі![]() Йигк
Йигк![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФБэДяЪНЃЛ
ЕФБэДяЪНЃЛ
ЃЈ3ЃЉШє![]() ЃЌЧѓжЄЃКЁАДцдкУПЯюЖМЪЧе§Ъ§ЕФЮоЧюЕШВюЪ§Са
ЃЌЧѓжЄЃКЁАДцдкУПЯюЖМЪЧе§Ъ§ЕФЮоЧюЕШВюЪ§Са![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() гы
гы![]() ОпгаЁЎЙВЩњЙиЯЕЁЏЁБЕФГфвЊЬѕМўЪЧЁАЕу
ОпгаЁЎЙВЩњЙиЯЕЁЏЁБЕФГфвЊЬѕМўЪЧЁАЕу![]() дкЩфЯп
дкЩфЯп![]() ЩЯЁБЃЎ
ЩЯЁБЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЈ2ЃЉЪЕЪ§Жд
ЃЈ2ЃЉЪЕЪ§Жд![]() ЫљЙЙГЩЕФМЏКЯЮЊ
ЫљЙЙГЩЕФМЏКЯЮЊ![]() ЃЌЧв
ЃЌЧв![]() ЃЌЦфжа
ЃЌЦфжа![]() ЃЌ
ЃЌ . ЃЈ3ЃЉжЄУїМћНтЮі.
. ЃЈ3ЃЉжЄУїМћНтЮі.
ЁОНтЮіЁП
(1) гЩ![]() ЃЌПЩжЊ
ЃЌПЩжЊ![]() ЃЌДгЖјПЩЕУ
ЃЌДгЖјПЩЕУ![]() .
.
(2) гЩЬтвтЕУ![]() ,ЕБ
,ЕБ![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌгы
ЪБЃЌгы![]() ЕФШЮвтСНЯюОљВЛЯрЕШЯрУЌЖм,ЙЪДЫЪБВЛКЯЬтвтЃЛЕБ
ЕФШЮвтСНЯюОљВЛЯрЕШЯрУЌЖм,ЙЪДЫЪБВЛКЯЬтвтЃЛЕБ![]() ЃЌ
ЃЌ![]() ЃЌВЛКЯЬтвтЃЌЕБ
ЃЌВЛКЯЬтвтЃЌЕБ![]() ЃЌвВВЛКЯЬтвт. Шє
ЃЌвВВЛКЯЬтвт. Шє![]() ЃЌдђ
ЃЌдђ![]() ЃЌгЩ
ЃЌгЩ![]() ЃЌ
ЃЌ![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌ
ЃЌ![]() ЕФШЮвтСНЯюОљВЛЯрЕШЃЌЙЪ
ЕФШЮвтСНЯюОљВЛЯрЕШЃЌЙЪ![]() ЃЌПЩжЊ
ЃЌПЩжЊ![]() ЃЌЕУГіД№АИ.
ЃЌЕУГіД№АИ.
(3)ЯШжЄБивЊадЃЌШє![]() ЪЧ
ЪЧ![]() ЙЋВюЕФЕШВюЪ§СаЃЌ
ЙЋВюЕФЕШВюЪ§СаЃЌ![]()
![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌЙЪ
ЃЌЙЪ НтЕУ
НтЕУ![]() ЃЌдйжЄГфЗжадЃЌШєЕу
ЃЌдйжЄГфЗжадЃЌШєЕу![]() дкЩфЯп
дкЩфЯп![]() ЩЯЃЌ
ЩЯЃЌ![]()
МД![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌДгЖјЕУжЄ.
ЃЌДгЖјЕУжЄ.
(1)гЩ![]() ЃЌПЩжЊ
ЃЌПЩжЊ![]()
ЫљвдгыЪ§Са![]() ОпгаЁАЙВЩњЙиЯЕЁБЕФКЏЪ§
ОпгаЁАЙВЩњЙиЯЕЁБЕФКЏЪ§![]() ЕФНтЮіЪНПЩвдЮЊЃК
ЕФНтЮіЪНПЩвдЮЊЃК![]() .
.
(2)гЩЬтвтЕУ![]() ЃЌСю
ЃЌСю![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌМД
ЃЌМД![]() .
.
ЂйШє![]() ЃЌДЫЪБВЛГЩСЂЃЌВЛКЯЬтвтЃЌ
ЃЌДЫЪБВЛГЩСЂЃЌВЛКЯЬтвтЃЌ
Шє![]() ЃЌгЩ
ЃЌгЩ![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌгж
ЃЌгж![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌгы
ЃЌгы![]() ЕФШЮвтСНЯюОљВЛЯрЕШЯрУЌЖм,ЙЪДЫЪБВЛКЯЬтвт.
ЕФШЮвтСНЯюОљВЛЯрЕШЯрУЌЖм,ЙЪДЫЪБВЛКЯЬтвт.
ЂкШє![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]()
Шє![]() ЃЌдђгЩ
ЃЌдђгЩ![]() гы
гы![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌВЛКЯЬтвт.
ЃЌВЛКЯЬтвт.
Шє![]() ЃЌдђ
ЃЌдђ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌВЛКЯЬтвт.
ЃЌВЛКЯЬтвт.
Шє![]() ЃЌдђ
ЃЌдђ![]() ЃЌгЩ
ЃЌгЩ![]() ЃЌ
ЃЌ![]()
ПЩЕУ![]() ЃЌМД
ЃЌМД![]()
ДЫЪБЪ§Са![]() ЪЧЪзЯюЮЊ
ЪЧЪзЯюЮЊ![]() ЃЌЙЋБШЮЊ
ЃЌЙЋБШЮЊ![]() ЕФЕШБШЪ§СаЃЌгж
ЕФЕШБШЪ§СаЃЌгж![]() ЕФШЮвтСНЯюОљВЛЯрЕШЃЌ
ЕФШЮвтСНЯюОљВЛЯрЕШЃЌ
ЙЪ![]() ЃЌПЩжЊ
ЃЌПЩжЊ![]()
ЫљвдЪЕЪ§Жд![]() ЫљЙЙГЩЕФМЏКЯЮЊ
ЫљЙЙГЩЕФМЏКЯЮЊ![]() ЃЌЧв
ЃЌЧв![]() ЃЌЦфжа
ЃЌЦфжа![]()

(3)(БивЊад)Шє![]() ЪЧ
ЪЧ![]() ЙЋВюЕФЕШВюЪ§СаЃЌЧвгы
ЙЋВюЕФЕШВюЪ§СаЃЌЧвгы![]() ОпгаЁАЙВЩњЙиЯЕЁБ.
ОпгаЁАЙВЩњЙиЯЕЁБ.
дђгЩ![]() ЃЌ
ЃЌ![]()
ПЩЕУ: ![]()
ЙЪ![]() ЃЌМД
ЃЌМД![]() КуГЩСЂ.
КуГЩСЂ.
ЙЪ НтЕУ
НтЕУ![]()
гжгЩ![]() ,ПЩЕУ
,ПЩЕУ![]() ,
,
гЩ![]() ,ПЩжЊ
,ПЩжЊ![]()
ЫљвдЕу![]() дкЩфЯп
дкЩфЯп![]() ЩЯ.
ЩЯ.
(ГфЗжад)ШєЕу![]() дкЩфЯп
дкЩфЯп![]() ЩЯЃЌдђ
ЩЯЃЌдђ![]()
гжЗНГЬ![]() ЕШМлгк
ЕШМлгк![]() ЃЌ
ЃЌ![]()
Чв![]() ЃЌШЁ
ЃЌШЁ![]() ЃЌЫќЯдШЛЪЧе§Ъ§ЧвТњзу
ЃЌЫќЯдШЛЪЧе§Ъ§ЧвТњзу![]()
Сю![]() ЃЌдђ
ЃЌдђ![]()
![]() ЃЌ
ЃЌ
ЙЪЕБ![]() ЪБЃЌ
ЪБЃЌ![]()
етРяЮоЧюЪ§Са![]() ЪЧЪзЯюЮЊ
ЪЧЪзЯюЮЊ![]() ЃЌЙЋВюЮЊ
ЃЌЙЋВюЮЊ![]() ЕФЮоЧюЕШВюЪ§Са.
ЕФЮоЧюЕШВюЪ§Са.
ЦфжаУПвЛЯюЖМЪЧе§Ъ§ЃЌЫљвдДцдкУПвЛЯюЖМЪЧе§Ъ§ЕФЮоЧюЕШВюЪ§Са![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() гы
гы![]() ОпгаЁАЙВЩњЙиЯЕЁБ.
ОпгаЁАЙВЩњЙиЯЕЁБ.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌСтаЮ![]() ЕФБпГЄЮЊ12ЃЌ
ЕФБпГЄЮЊ12ЃЌ![]() ЃЌ
ЃЌ![]() гы
гы![]() НЛгк
НЛгк![]() ЕуЃЌНЋСтаЮ
ЕуЃЌНЋСтаЮ![]() биЖдНЧЯп
биЖдНЧЯп![]() елЦ№ЃЌЕУЕНШ§РтзЖ
елЦ№ЃЌЕУЕНШ§РтзЖ![]() ЃЌЕу
ЃЌЕу![]() ЪЧРт
ЪЧРт![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЃЎ
ЃЎ
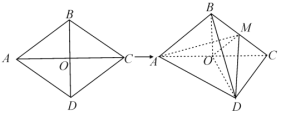
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓЖўУцНЧ![]() ЕФгрЯвжЕЃЎ
ЕФгрЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊжБЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ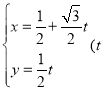 ЮЊВЮЪ§ЃЉЃЌвдзјБъдЕуЮЊМЋЕуЃЌ
ЮЊВЮЪ§ЃЉЃЌвдзјБъдЕуЮЊМЋЕуЃЌ![]() жсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЧњЯп
жсЕФе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЧњЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() .
.
ЃЈ1ЃЉЧѓжБЯп![]() ЕФЦеЭЈЗНГЬКЭЧњЯп
ЕФЦеЭЈЗНГЬКЭЧњЯп![]() ЕФжБНЧзјБъЗНГЬЃЛ
ЕФжБНЧзјБъЗНГЬЃЛ
ЃЈ2ЃЉЩшЕу![]() ЃЌжБЯп
ЃЌжБЯп![]() гыЧњЯп
гыЧњЯп![]() НЛгк
НЛгк![]() СНЕуЃЌЧѓ
СНЕуЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПАЃМАН№зжЫўЪЧЙХАЃМАЕФЕлЭѕЃЈЗЈРЯЃЉСъФЙЃЌЪРНчЦпДѓЦцМЃжЎвЛЃЌЦфжаНЯЮЊжјУћЕФЪЧКњЗђН№зжЫўЃЎСюШЫГдОЊЕФВЂВЛНіНіЪЧКњЗђН№зжЫўЕФалзГЩэзЫЃЌЛЙгаЗЂЩњдкКњЗђН№зжЫўЩЯЕФЪ§зжЁАЧЩКЯЁБЃЎШчКњЗђН№зжЫўЕФЕзВПжмГЄШчЙћГ§вдЦфИпЖШЕФСНБЖЃЌЕУЕНЕФЩЬЮЊ3.14159ЃЌетОЭЪЧдВжмТЪНЯЮЊОЋШЗЕФНќЫЦжЕЃЎН№зжЫўЕзВПаЮЮЊе§ЗНаЮЃЌећИіЫўаЮЮЊе§ЫФРтзЖЃЌОЙХДњФмЙЄЧЩНГНЈЩшЭъГЩКѓЃЌЕззљБпГЄДѓдМ230УзЃЎвђФъОУЗчЛЏЃЌЖЅЖЫАўТф10УзЃЌдђКњЗђН№зжЫўЯжИпДѓдМЮЊЃЈ ЃЉ
A.128.5УзB.132.5УзC.136.5УзD.110.5Уз
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЁао4-4ЃКзјБъЯЕгыВЮЪ§ЗНГЬ
дкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЧњЯп
жаЃЌЧњЯп![]() Й§Еу
Й§Еу![]() ЃЌЦфВЮЪ§ЗНГЬЮЊ
ЃЌЦфВЮЪ§ЗНГЬЮЊ ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЌ
ЮЊВЮЪ§ЃЌ![]() ЃЉЃЌвд
ЃЉЃЌвд![]() ЮЊМЋЕуЃЌ
ЮЊМЋЕуЃЌ![]() жсЗЧИКАыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЧњЯп
жсЗЧИКАыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЧњЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() .
.
ЃЈ1ЃЉЧѓЧњЯп![]() ЕФЦеЭЈЗНГЬКЭЧњЯп
ЕФЦеЭЈЗНГЬКЭЧњЯп![]() ЕФжБНЧзјБъЗНГЬЃЛ
ЕФжБНЧзјБъЗНГЬЃЛ
ЃЈ2ЃЉЧѓвбжЊЧњЯп![]() КЭЧњЯп
КЭЧњЯп![]() НЛгк
НЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌЧв
СНЕуЃЌЧв![]() ЃЌЧѓЪЕЪ§
ЃЌЧѓЪЕЪ§![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯп![]() ЕФЖЅЕуЪЧЭждВ
ЕФЖЅЕуЪЧЭждВ![]() ЕФжааФЃЌНЙЕугыИУЭждВЕФгвНЙЕужиКЯ.
ЕФжааФЃЌНЙЕугыИУЭждВЕФгвНЙЕужиКЯ.
ЃЈ1ЃЉЧѓХзЮяЯп![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉвбжЊЖЏжБЯп![]() Й§Еу
Й§Еу![]() ЃЌНЛХзЮяЯп
ЃЌНЛХзЮяЯп![]() гк
гк![]() ЃЌ
ЃЌ![]() СНЕуЃЌзјБъдЕу
СНЕуЃЌзјБъдЕу![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌЧѓжЄ
ЕФжаЕуЃЌЧѓжЄ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЪЧЗёДцдкДЙжБгк![]() жсЕФжБЯп
жсЕФжБЯп![]() БЛвд
БЛвд![]() ЮЊжБОЖЕФдВЫљНиЕУЕФЯвГЄКуЮЊЖЈжЕЃПШчЙћДцдкЃЌЧѓГі
ЮЊжБОЖЕФдВЫљНиЕУЕФЯвГЄКуЮЊЖЈжЕЃПШчЙћДцдкЃЌЧѓГі![]() ЕФЗНГЬЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФЗНГЬЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() Й§Еу
Й§Еу![]() ЃЌЧвЫќЕФвЛИіНЙЕугыХзЮяЯп
ЃЌЧвЫќЕФвЛИіНЙЕугыХзЮяЯп![]() ЕФНЙЕуЯрЭЌЃЎжБЯп
ЕФНЙЕуЯрЭЌЃЎжБЯп![]() Й§Еу
Й§Еу![]() ЃЌЧвгыЭждВ
ЃЌЧвгыЭждВ![]() ЯрНЛгк
ЯрНЛгк![]() СНЕуЃЎ
СНЕуЃЎ
ЃЈ1ЃЉЧѓЭждВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉШєжБЯп![]() ЕФвЛИіЗНЯђЯђСПЮЊ
ЕФвЛИіЗНЯђЯђСПЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФУцЛ§ЃЈЦфжа
ЕФУцЛ§ЃЈЦфжа![]() ЮЊзјБъдЕуЃЉЃЛ
ЮЊзјБъдЕуЃЉЃЛ
ЃЈ3ЃЉЪдЮЪЃКдк![]() жсЩЯЪЧЗёДцдкЕу
жсЩЯЪЧЗёДцдкЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЮЊЖЈжЕЃПШєДцдкЃЌЧѓГіЕу
ЮЊЖЈжЕЃПШєДцдкЃЌЧѓГіЕу![]() ЕФзјБъКЭЖЈжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъКЭЖЈжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВCЃК![]() ЕФЖЬжсГЄЮЊ2ЃЌРыаФТЪЮЊ
ЕФЖЬжсГЄЮЊ2ЃЌРыаФТЪЮЊ![]() ЃЌзѓЖЅЕуЮЊAЃЌЙ§ЕуAЕФжБЯпlгыCНЛгкСэвЛИіЕуMЃЌЧвгыжБЯпxЃНtНЛгкЕуNЃЎ
ЃЌзѓЖЅЕуЮЊAЃЌЙ§ЕуAЕФжБЯпlгыCНЛгкСэвЛИіЕуMЃЌЧвгыжБЯпxЃНtНЛгкЕуNЃЎ
ЃЈ1ЃЉЧѓЭждВCЕФЗНГЬЃЛ
ЃЈ2ЃЉЪЧЗёДцдкЪЕЪ§tЃЌЪЙЕУ![]() ЮЊЖЈжЕЃПШєДцдкЃЌЧѓЪЕЪ§tЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЮЊЖЈжЕЃПШєДцдкЃЌЧѓЪЕЪ§tЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са{an}ЕФИїЯюОљЮЊе§Ъ§ЃЌЦфЧАnЯюКЭSnТњзу4SnЃНan2+2anЃЌnЁЪN*.ЩшbnЃНЃЈЉ1ЃЉnanan+1ЃЌTnЮЊЪ§Са{bn}ЕФЧАnЯюКЭЃЌдђT2nЃН_____.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com