练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】甲、乙两个排球队在采用局胜制排球决赛中相遇，已知每局比赛中甲获胜的概率是.

    （1）求比赛进行了局就结束的概率；

    （2）若第局甲胜，两队又继续进行了局结束比赛，求的分布列和数学期望

    【答案】（1）；（2）分布列见解析，.

    【解析】

    （1）根据题意可知，比赛进行了局就结束包含两种情况：一是局全都是甲赢，二是局全都是乙赢，然后利用独立事件的概率乘法公式可计算出所求事件的概率；

    （2）由题意可知，随机变量的可能取值有、、，利用独立事件的概率乘法公式计算出在不同取值下的概率，可得出随机变量的概率分布列，进而可计算出随机变量的数学期望.

    （1）由题意知，每局比赛中乙胜的概率是，比赛进行了局就结束包括甲胜和乙胜两种情况，所以所求概率为；

    （2）由题意知的可能取值为、、，

    ，，

    .

    所以，随机变量的分布列为

    所以.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左、右焦点分别为，是椭圆上一动点（与左、右顶点不重合）已知的内切圆半径的最大值为，椭圆的离心率为.

    （1）求椭圆C的方程；

    （2）过的直线交椭圆于两点，过作轴的垂线交椭圆与另一点（不与重合）.设的外心为，求证为定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司组织开展“学习强国”的学习活动，活动第一周甲、乙两个部门员工的学习情况统计如下：

    学习活跃的员工人数

    学习不活跃的员工人数

    甲

    18

    12

    乙

    32

    8

    （1）从甲、乙两个部门所有员工中随机抽取1人，求该员工学习活跃的概率；

    （2）根据表中数据判断能否有的把握认为员工学习是否活跃与部门有关；

    （3）活动第二周，公司为检查学习情况，从乙部门随机抽取2人，发现这两人学习都不活跃，能否认为乙部门第二周学习的活跃率比第一周降低了？

    参考公式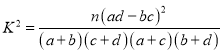：，其中.

    参考数据：，，.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示的几何体中，是菱形，，平面，，.

    （1）求证：平面平面；

    （2）求平面与平面构成的二面角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，函数（其中是自然对数的底数，）．

    （1）当时，求曲线在点处的切线方程；

    （2）若当时都有成立，求整数的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆经过点，右焦点到直线的距离为3．

    （1）求椭圆E的标准方程；

    （2）过点A作两条互相垂直的直线，分别交椭圆于M，N两点，求证：直线MN恒过定点．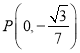

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，以原点O为极点，x轴的正半轴为极轴，建立极坐标系，曲线C的极坐标方程为．

    （1）求曲线C的普通方程；

    （2）直线l的参数方程为，（t为参数），直线l与x轴交于点F，与曲线C的交点为A，B，当取最小值时，求直线l的直角坐标方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4—5: 不等式选讲

    已知函数f(x)＝ 的定义域为R.

    (Ⅰ)求实数m的取值范围；

    (Ⅱ)若m的最大值为n，当正数a，b满足 ＝n时，求7a＋4b的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】椭圆的离心率为，以原点为圆心，椭圆短半轴长为半径的圆与直线相切．

    （1）求椭圆的方程；

    （2）M，N是椭圆上关于x轴对称的两点，P是椭圆上不同于M，N的一点，直线PM，PN交x轴于D（xD，0）E（xE，0），证明：xDxE为定值．

    查看答案和解析>>

    同步练习册答案