
【题目】已知动圆过定点P(4,0),且在y轴上截得的弦MN的长为8.
(1)求动圆圆心C的轨迹方程;
(2)过点(2,0)的直线l与动圆圆心C的轨迹交于A,B两点,求证:![]() 是一个定值.
是一个定值.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)设圆心的坐标为![]() ,得出
,得出![]() ,代入点的坐标,即可得到曲线C的轨迹方程;
,代入点的坐标,即可得到曲线C的轨迹方程;
(2)设直线方程![]() ,联立方程组,得到
,联立方程组,得到![]() ,再向量的数量积的运算,即可得到结论.
,再向量的数量积的运算,即可得到结论.
(1)设动圆的圆心C(x,y),线段MN的中点为T,则|MT|=![]() =4.
=4.
由题意得|CP|2=|CM|2=|MT|2+|TC|2,∴y2+(x-4)2=42+x2,∴y2=8x,
即动圆圆心C的轨迹方程为y2=8x.
(2)证明:易知直线l的斜率不为0,
设直线l的方程为x=ky+2,A(x1,y1),B(x2,y2).
联立![]() 消去x整理得y2-8ky-16=0,Δ=64k2+64>0,可得y1+y2=8k,y1y2=-16.
消去x整理得y2-8ky-16=0,Δ=64k2+64>0,可得y1+y2=8k,y1y2=-16.
又![]() =(x1,y1),
=(x1,y1),![]() =(x2,y2),
=(x2,y2),
∴![]() ·
·![]() =x1x2+y1y2=(ky1+2)(ky2+2)+y1y2=k2y1y2+2k(y1+y2)+4+y1y2=-16k2+16k2+4-16=-12,
=x1x2+y1y2=(ky1+2)(ky2+2)+y1y2=k2y1y2+2k(y1+y2)+4+y1y2=-16k2+16k2+4-16=-12,
∴![]() ·
·![]() 是一个定值.
是一个定值.


科目:高中数学 来源: 题型:
【题目】某个体服装店经营某种服装,该服装店每天所获利润y(元)与每天售出这种服装件数x之间的一组数据关系如下表:
x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
y | 66 | 69 | 74 | 81 | 89 | 90 | 91 |
(1)求利润y与每天售出件数x之间的回归方程 (回归直线的斜率用分数表示).
(2)若该服装店某天销售服装13件,估计可获利润多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,江的两岸可近似的看成两平行的直线,江岸的一侧有A,B两个蔬菜基地,江的另一侧点C处有一个超市.已知A、B、C中任意两点间的距离为20千米.超市欲在AB之间建一个运输中转站D,A,B两处的蔬菜运抵D处后,再统一经过货轮运抵C处.由于A,B两处蔬菜的差异,这两处的运输费用也不同.如果从A处出发的运输费为每千米2元,从B处出发的运输费为每千米1元,货轮的运输费为每千米3元. 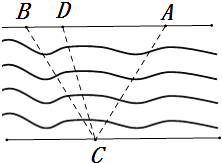
(1)设∠ADC=α,试将运输总费用S(单位:元)表示为α的函数S(α),并写出自变量的取值范围;
(2)问中转站D建在何处时,运输总费用S最小?并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知恒等式(1+x+x2)n=a0+a1x+a2x2+…+a2nx2n .
(1)求a1+a2+a3+…+a2n和a2+2a3+22a4+…+22n﹣2a2n的值;
(2)当n≥6时,求证: ![]() a2+2A
a2+2A ![]() a3+…+22n﹣2
a3+…+22n﹣2 ![]() a2n<49n﹣2 .
a2n<49n﹣2 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PC⊥平面PAD,AB∥CD,CD=2AB=2BC,M,N分别是棱PA,CD的中点. 
(1)求证:PC∥平面BMN;
(2)求证:平面BMN⊥平面PAC. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=xex﹣asinxcosx(a∈R,其中e是自然对数的底数).
(1)当a=0时,求f(x)的极值;
(2)若对于任意的x∈[0, ![]() ],f(x)≥0恒成立,求a的取值范围;
],f(x)≥0恒成立,求a的取值范围;
(3)是否存在实数a,使得函数f(x)在区间 ![]() 上有两个零点?若存在,求出a的取值范围;若不存在,请说明理由.
上有两个零点?若存在,求出a的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是公差为正数的等差数列,其前
是公差为正数的等差数列,其前![]() 项和为
项和为![]() ,
,
且![]() ,
,![]()
(1)求数列![]() 的通项公式.
的通项公式.
(2)设数列![]() 满足
满足![]() ,
,![]()
①求数列![]() 的通项公式;
的通项公式;
②是否存在正整数![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等差数列?若存在,求出
成等差数列?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com