
【题目】已知函数![]() .
.
(1)当![]() 时,如果函数
时,如果函数![]() 仅有一个零点,求实数
仅有一个零点,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,试比较
时,试比较![]() 与1的大小;
与1的大小;
(3)求证:![]()
![]()
【答案】(1)![]() 的取值范围是
的取值范围是![]() 或
或![]() ;(2)①当
;(2)①当![]() 时,
时,![]() ,即
,即![]() ;
;
②当![]() 时,
时,![]() ,即
,即![]() ;③当
;③当![]() 时,
时,![]() ,即
,即![]() ;(3)证明过程详见解析.
;(3)证明过程详见解析.
【解析】试题分析:本题考查函数与导数、导数的运算、利用导数判断函数的单调性、利用导数求函数的极值与最值等数学知识和方法,考查综合运用数学知识和方法分析问题和解决问题的能力,考查函数思想和分类讨论思想.第一问,先将![]() 代入得到
代入得到![]() 解析式,因为
解析式,因为![]() 仅有一个零点,所以
仅有一个零点,所以![]() 和
和![]() 仅有一个交点,所以关键是
仅有一个交点,所以关键是![]() 的图像,对
的图像,对![]() 求导,令
求导,令![]() 和
和![]() 判断函数的单调性,确定函数的极值和最值所在位置,求出具体的数值,便可以描绘出函数图像,来决定
判断函数的单调性,确定函数的极值和最值所在位置,求出具体的数值,便可以描绘出函数图像,来决定![]() 的位置;第二问,先将
的位置;第二问,先将![]() 代入,得到
代入,得到![]() 解析式,作差法比较大小,得到新函数
解析式,作差法比较大小,得到新函数![]() ,判断
,判断![]() 的正负即可,通过对
的正负即可,通过对![]() 求导,可以看出
求导,可以看出![]() 在
在![]() 上是增函数且
上是增函数且![]() ,所以分情况会出现3种大小关系;第三问,法一:利用第二问的结论,得到表达式
,所以分情况会出现3种大小关系;第三问,法一:利用第二问的结论,得到表达式![]() ,再利用不等式的性质得到所证表达式的右边,左边是利用对数的运算性质化简,得证;法二,用数学归纳法证明,先证明当
,再利用不等式的性质得到所证表达式的右边,左边是利用对数的运算性质化简,得证;法二,用数学归纳法证明,先证明当![]() 时不等式成立,再假设当
时不等式成立,再假设当![]() 时不等式成立,然后利用假设的结论证明当
时不等式成立,然后利用假设的结论证明当![]() 时不等式成立即可.
时不等式成立即可.
试题解析:(1)当![]() 时,
时,![]() ,定义域是
,定义域是![]() ,
,
![]() ,令
,令![]() ,得
,得![]() 或
或![]() .
.
∵当![]() 或
或![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() 的极大值是
的极大值是![]() ,极小值是
,极小值是![]() .
.
∵当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
![]() 当
当![]() 仅有一个零点时,
仅有一个零点时,![]() 的取值范围是
的取值范围是![]() 或
或![]() . 4分
. 4分
(2)当![]() 时,
时,![]() ,定义域为
,定义域为![]() .
.
令![]() ,
,
![]() ,
,
![]() 在
在![]() 上是增函数.
上是增函数.
①当![]() 时,
时,![]() ,即
,即![]() ;
;
②当![]() 时,
时,![]() ,即
,即![]() ;
;
③当![]() 时,
时,![]() ,即
,即![]() . 8分
. 8分
(3)(法一)根据(2)的结论,当![]() 时,
时,![]() ,即
,即![]() .
.
令![]() ,则有
,则有![]() ,
,
![]() .
.![]() ,
,
![]() . 12分
. 12分
(法二)当![]() 时,
时,![]() .
.
![]() ,
,![]() ,即
,即![]() 时命题成立.
时命题成立.
设当![]() 时,命题成立,即
时,命题成立,即![]() .
.
![]() 时,
时,![]()
![]() .
.
根据(2)的结论,当![]() 时,
时,![]() ,即
,即![]() .
.
令![]() ,则有
,则有![]() ,
,
则有![]() ,即
,即![]() 时命题也成立.
时命题也成立.
因此,由数学归纳法可知不等式成立.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
【题目】袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为![]() .现在甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取…取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的.
.现在甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取…取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的.
(1)求袋中原有白球的个数;
(2)求取球两次终止的概率
(3)求甲取到白球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭记录了未使用节水龙头50天的日用水量数据(单位:m3)和使用了节水龙头50天的日用水量数据,得到频数分布表如下:
未使用节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
|
频数 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
使用了节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
频数 | 1 | 5 | 13 | 10 | 16 | 5 |
(1)在答题卡上作出使用了节水龙头50天的日用水量数据的频率分布直方图:
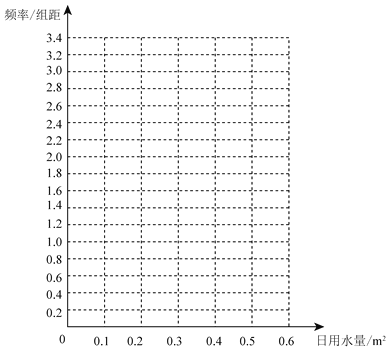
(2)估计该家庭使用节水龙头后,日用水量小于0.35 m3的概率;
(3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.已知点
轴的正半轴为极轴建立极坐标系.已知点![]() 的直角坐标为
的直角坐标为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 过点
过点![]() 且与曲线
且与曲线![]() 相交于
相交于![]() ,
,![]() 两点.
两点.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() ,求直线
,求直线![]() 的直角坐标方程.
的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表,即杨辉三角,这是数学史上的一个伟大成就.在“杨辉三角”中,已知第![]() 行的所有数字之和为
行的所有数字之和为![]() ,若去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,……,则此数列的前56项和为( )
,若去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,……,则此数列的前56项和为( )

A. 2060B. 2038C. 4084D. 4108
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线x2=2py(p>0)上的点M(m,1)到焦点F的距离为2, 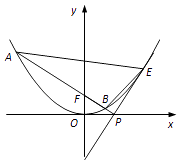
(1)求抛物线的方程;
(2)如图,点E是抛物线上异于原点的点,抛物线在点E处的切线与x轴相交于点P,直线PF与抛物线相交于A,B两点,求△EAB面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小陈同学进行三次定点投篮测试,已知第一次投篮命中的概率为![]() ,第二次投篮命中的概率为
,第二次投篮命中的概率为![]() ,前两次投篮是否命中相互之间没有影响.第三次投篮受到前两次结果的影响,如果前两次投篮至少命中一次,则第三次投篮命中的概率为
,前两次投篮是否命中相互之间没有影响.第三次投篮受到前两次结果的影响,如果前两次投篮至少命中一次,则第三次投篮命中的概率为![]() ,否则为
,否则为![]() .
.
(1)求小陈同学三次投篮至少命中一次的概率;
(2)记小陈同学三次投篮命中的次数为随机变量![]() ,求
,求![]() 的概率分布及数学期望.
的概率分布及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某学校高三年级共800名男生中随机抽取50人测量身高.据测量,被测学生身高全部介于![]() 到
到![]() 之间,将测量结果按如下方式分成八组:第一组
之间,将测量结果按如下方式分成八组:第一组![]() ;第二组
;第二组![]() ;…;第八组
;…;第八组![]() .如图是按上述分组方法得到的频率分布直方图的一部分.已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
.如图是按上述分组方法得到的频率分布直方图的一部分.已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.

(1)估计这所学校高三年级全体男生身高在![]() 以上(含
以上(含![]() )的人数;
)的人数;
(2)求第六组、第七组的频率并补充完整频率分布直方图;
(3)若从身高属于第六组和第八组的所有男生中随机抽取两人,记他们的身高分别为![]() ,求满足“
,求满足“![]() ”的事件的概率.
”的事件的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com