
【题目】已知函数![]() ,
, ![]() .
.
(1)求函数![]() 的极值;
的极值;
(2)若不等式![]() 对
对![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)答案见解析;(2) ![]() .
.
【解析】试题分析:(1)对函数求导得到![]()
![]() ,讨论
,讨论![]() 和0和1 的大小关系,在不同情况下求得导函数的正负即得到原函数的单调性,根据极值的概念得到结果;(2)设
和0和1 的大小关系,在不同情况下求得导函数的正负即得到原函数的单调性,根据极值的概念得到结果;(2)设![]()
![]() ,构造以上函数,研究函数的单调性,求得函数的最值,使得最小值大于等于0即可.
,构造以上函数,研究函数的单调性,求得函数的最值,使得最小值大于等于0即可.
解析:
(Ⅰ)![]() ,
,
![]()
![]() ,
,
∵![]() 的定义域为
的定义域为![]() .
.
①![]() 即
即![]() 时,
时, ![]() 在
在![]() 上递减,
上递减, ![]() 在
在![]() 上递增,
上递增,
![]() ,
, ![]() 无极大值.
无极大值.
②![]() 即
即![]() 时,
时, ![]() 在
在![]() 和
和![]() 上递增,在
上递增,在![]() 上递减,
上递减,
![]()
![]() ,
, ![]() .
.
③![]() 即
即![]() 时,
时, ![]() 在
在![]() 上递增,
上递增, ![]() 没有极值.
没有极值.
④![]() 即
即![]() 时,
时, ![]() 在
在![]() 和
和![]() 上递增,
上递增, ![]() 在
在![]() 上递减,
上递减,
∴![]() ,
, ![]()
![]() .
.
综上可知: ![]() 时,
时, ![]() ,
, ![]() 无极大值;
无极大值;
![]() 时,
时, ![]()
![]() ,
, ![]() ;
;
![]() 时,
时, ![]() 没有极值;
没有极值;
![]() 时,
时, ![]() ,
, ![]()
![]() .
.
(Ⅱ)设![]()
![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
, ![]() ,
, 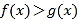
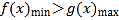 ,
,
∴![]() 在
在![]() 上递增,∴
上递增,∴![]() 的值域为
的值域为![]() ,
,
①当![]() 时,
时, ![]() ,
, ![]() 为
为![]() 上的增函数,
上的增函数,
∴![]() ,适合条件.
,适合条件.
②当![]() 时,∵
时,∵![]() ,∴不适合条件.
,∴不适合条件.
③当![]() 时,对于
时,对于![]() ,
, ![]() ,
,
令![]() ,
, ![]() ,
,
存在![]() ,使得
,使得![]() 时,
时, ![]() ,
,
∴![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,
,
即在![]() 时,
时, ![]() ,∴不适合条件.
,∴不适合条件.
综上, ![]() 的取值范围为
的取值范围为![]() .
.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,过F且斜率为![]() 的直线l与抛物线C交于A,B两点,B在x轴的上方,且点B的横坐标为4.
的直线l与抛物线C交于A,B两点,B在x轴的上方,且点B的横坐标为4.
(1)求抛物线C的标准方程;
(2)设点P为抛物线C上异于A,B的点,直线PA与PB分别交抛物线C的准线于E,G两点,x轴与准线的交点为H,求证:HGHE为定值,并求出定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正四面体ABCD中,点E,F分别是AB,BC的中点,则下列命题正确的序号是______
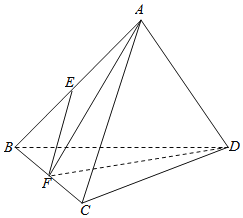
①异面直线AB与CD所成角为90°;
②直线AB与平面BCD所成角为60°;
③直线EF∥平面ACD
④平面AFD⊥平面BCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某面包推出一款新面包,每个面包的成本价为4元,售价为10元,该款面包当天只出一炉(一炉至少15个,至多30个),当天如果没有售完,剩余的面包以每个2元的价格处理掉,为了确定这一炉面包的个数,该店记录了这款新面包最近30天的日需求量(单位:个),整理得下表:

(1)根据表中数据可知,频数![]() 与日需求量
与日需求量![]() (单位:个)线性相关,求
(单位:个)线性相关,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)以30天记录的各日需求量的频率代替各日需求量的概率,若该店这款新面包出炉的个数为24,记当日这款新面包获得的总利润为![]() (单位:元).
(单位:元).
(ⅰ)若日需求量为15个,求![]() ;
;
(ⅱ)求![]() 的分布列及其数学期望.
的分布列及其数学期望.
相关公式: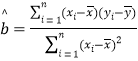
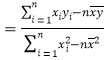 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的图象为C,则下列结论中正确的是( )
的图象为C,则下列结论中正确的是( )
A.图象C关于直线![]() 对称
对称
B.图象C关于点![]() 对称
对称
C.函数![]() 在区间
在区间![]() 内是增函数
内是增函数
D.把函数![]() 的图象上点的横坐标缩短为原来的一半(纵坐标不变)可以得到图象C
的图象上点的横坐标缩短为原来的一半(纵坐标不变)可以得到图象C
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥![]() 中,四边形
中,四边形![]() 为矩形,
为矩形, ![]() 为等腰三角形,
为等腰三角形, ![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 的中点.
的中点.

(1)证明: ![]() 平面
平面![]() ;
;
(2)证明:平面![]() 平面
平面![]() ;
;
(3)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面,BC=![]() ,M为BC的中点.
,M为BC的中点.
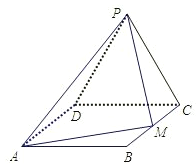
(I)证明:AM⊥PM ;
(II)求二面角P-AM-D的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com