
 等于( )
等于( )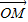
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
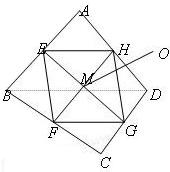 已知E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点.
已知E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点.| OM |
| 1 |
| 4 |
| OA |
| OB |
| OC |
| OD |
查看答案和解析>>
科目:高中数学 来源: 题型:
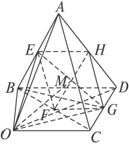
(1)用向量法证明E、F、G、H四点共面;
(2)用向量法证明BD∥平面EFGH;
(3)设M是EG和FH的交点,求证:对空间任一点O,有![]() =
=![]() (
(![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
![]() 已知E、F、G、H分别是空间四边形ABCD的边AB、BC、CD、DA的中点.
已知E、F、G、H分别是空间四边形ABCD的边AB、BC、CD、DA的中点.
(1)用向量法证明E、F、G、H四点共面;
(2)用向量法证明: BD∥平面EFGH;
(3)设M是EG和FH的交点,
求证:对空间任一点O,有![]() .
.
查看答案和解析>>
科目:高中数学 来源:2012年苏教版高中数学选修2-1 3.1空间向量及其坐标运算练习卷(解析版) 题型:解答题
已知E、F、G、H分别是空间四边形ABCD的边AB、BC、CD、DA的中点,
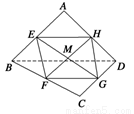
(1)求证:E、F、G、H四点共面;
(2)求证:BD∥平面EFGH;
(3)设M是EG和FH的交点,求证:对空间任一点O,有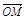 =
= (
( +
+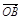 +
+ +
+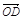 ).
).
查看答案和解析>>
科目:高中数学 来源:高考数学一轮复习必备(第76课时):第九章 直线、平面、简单几何体-空间向量及其运算(解析版) 题型:解答题
 已知E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点.
已知E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA的中点. .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com