
【题目】如图,四棱锥![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() .
.
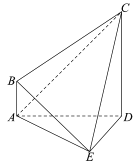
(1)求棱锥![]() 的体积;
的体积;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)![]() ;
;
(2)见试题解析;
(3)在线段![]() 上存在一点
上存在一点![]() ,且
,且![]() ,使
,使![]() 平面
平面![]() 。
。
【解析】
试题(I)在在![]() 中,
中,![]() ,可得
,可得![]() ,由于
,由于![]() 平面
平面![]() ,可的棱锥的高,利用体积公式求解几何体的体积;(II)由
,可的棱锥的高,利用体积公式求解几何体的体积;(II)由![]() 平面
平面![]() ,可得
,可得![]() ,进而得到
,进而得到![]() 平面
平面![]() ,即可证明平面
,即可证明平面![]()
![]() 平面
平面![]() ;(III)在线段
;(III)在线段![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 平面
平面![]() ,
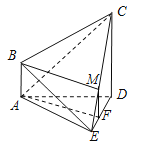
,![]() ,设F为线段DE上的一点,且
,设F为线段DE上的一点,且![]() ,过F作
,过F作![]() ,由线面垂直的性质可得
,由线面垂直的性质可得![]() ,可得四边形ABMF是平行四边形,于是
,可得四边形ABMF是平行四边形,于是![]() ,即可证明
,即可证明![]() 平面
平面![]() .
.
试题解析:(Ⅰ)在![]() 中,
中,![]()
因为![]() 平面
平面![]() ,
,
所以棱锥![]() 的体积为
的体积为![]() .
.
(Ⅱ)证明:因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() .又因为
.又因为![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .又因为
.又因为![]() 平面
平面![]() ,
,
所以平面![]()
![]() 平面
平面![]() .
.
(Ⅲ)结论:在线段![]() 上存在一点
上存在一点![]() ,且
,且![]() ,
,
使![]() 平面
平面![]() .
.
解:设![]() 为线段
为线段![]() 上一点, 且
上一点, 且![]() , 过点
, 过点![]() 作
作![]() 交
交![]() 于
于![]() ,
,
则![]() .因为
.因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() .
.
又因为![]() 所以
所以![]() ,
,![]() ,所以四边形
,所以四边形![]() 是平行四边形,
是平行四边形,
则![]() .又因为
.又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.


科目:高中数学 来源: 题型:
【题目】为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效的改良玉米品种,为农民提供技术支.现对已选出的一组玉米的茎高进行统计,获得茎叶图如右图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.

(1)完成![]() 列联表,并判断是否可以在犯错误的概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?
列联表,并判断是否可以在犯错误的概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?
(2)①按照分层抽样的方式,在上述样本中,从易倒伏和抗倒伏两组中抽取9株玉米,设取出的易倒伏矮茎玉米株数为![]() ,求
,求![]() 的分布列(概率用组合数算式表示);
的分布列(概率用组合数算式表示);
②若将频率视为概率,从抗倒伏的玉米试验田中再随机抽取出50株,求取出的高茎玉米株数的数学期望和方差.


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修![]() :坐标系与参数方程
:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为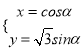 (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴的正半轴为极轴,建立极坐标系.曲线
轴的正半轴为极轴,建立极坐标系.曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,求
上,求![]() 的最小值及此时点
的最小值及此时点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
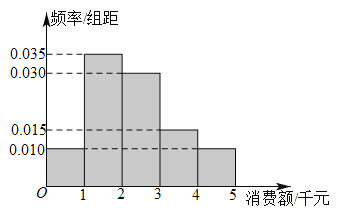
【题目】某商场在“五一”促销活动中,为了了解消费额在5千元以下(含5千元)的顾客的消费分布情况,从这些顾客中随机抽取了100位顾客的消费数据(单位:千元),按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成5组,制成了如图所示的频率分布直方图现采用分层抽样的方法从
分成5组,制成了如图所示的频率分布直方图现采用分层抽样的方法从![]() 和
和![]() 两组顾客中抽取4人进行满意度调查,再从这4人中随机抽取2人作为幸运顾客,求所抽取的2位幸运顾客都来自
两组顾客中抽取4人进行满意度调查,再从这4人中随机抽取2人作为幸运顾客,求所抽取的2位幸运顾客都来自![]() 组的概率.
组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,其中
,其中![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 单调递增区间;
单调递增区间;
(2)求证:对任意![]() ,函数
,函数![]() 的图象在点
的图象在点![]() 处的切线恒过定点;
处的切线恒过定点;
(3)是否存在实数![]() 的值,使得
的值,使得![]() 在
在![]() 上有最大值或最小值,若存在,求出实数
上有最大值或最小值,若存在,求出实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】实验杯足球赛采用七人制淘汰赛规则,某场比赛中一班与二班在常规时间内战平,直接进入点球决胜环节,在点球决胜环节中,双方首先轮流罚点球三轮,罚中更多点球的球队获胜;若双方在三轮罚球中未分胜负,则需要进行一对一的点球决胜,即双方各派处一名队员罚点球,直至分出胜负;在前三轮罚球中,若某一时刻胜负已分,尚未出场的队员无需出场罚球(例如一班在先罚球的情况下,一班前两轮均命中,二班前两轮未能命中,则一班、二班的第三位同学无需出场).由于一班同学平时踢球热情较高,每位队员罚点球的命中率都能达到0.8,而二班队员的点球命中串只有0.5,比赛时通过抽签决定一班在每一轮都先罚球.
(1)定义事件![]() 为“一班第三位同学没能出场罚球”,求事件
为“一班第三位同学没能出场罚球”,求事件![]() 发生的概率;
发生的概率;
(2)若两队在前三轮点球结束后打平,则进入一对一点球决胜,一对一球决胜由没有在之前点球大战中出场过的队员主罚点球,若在一对一点球决胜的某一轮中,某对队员射入点球且另一队员未能射入,则比赛结束;若两名队员均射入或者均射失点球,则进行下一轮比赛. 若直至双方场上每名队员都已经出场罚球,则比赛亦结束,双方通过抽签决定胜负,本场比赛中若已知双方在点球大战,以随机变量![]() 记录双方进行一对一点球决胜的轮数,求
记录双方进行一对一点球决胜的轮数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以坐标原点
),以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,建立极坐标系,直线
轴的非负半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)设![]() 是曲线
是曲线![]() 上的一个动眯,当
上的一个动眯,当![]() 时,求点
时,求点![]() 到直线
到直线![]() 的距离的最小值;
的距离的最小值;
(2)若曲线![]() 上所有的点都在直线
上所有的点都在直线![]() 的右下方,求实数
的右下方,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com