
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 直接利用新定义得到关于z的等式,求得z后得答案.
解答 解:由题意可得,$|{\begin{array}{l}z&{1+i}\\{-i}&{2i}\end{array}}|=0$,
得:z•2i+i(1+i)=0,
即z=$\frac{1-i}{2i}$=$\frac{(1-i)i}{2{i}^{2}}$=$\frac{1+i}{-2}$=-$\frac{1}{2}$-$\frac{1}{2}$i,
故$\overline{z}$=-$\frac{1}{2}$+$\frac{1}{2}$i
∴复数$\overline{z}$对应的点的坐标的坐标为(-$\frac{1}{2}$,$\frac{1}{2}$)在第二象限.
故选:B.
点评 本题是新定义题,考查复数的代数表示法及其几何意义,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 25x2+36y2=1 | B. | 50x2+72y2=1 | C. | 10x2+24y2=1 | D. | $\frac{{2{x^2}}}{25}+\frac{{8{y^2}}}{9}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
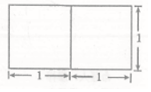 一个底面是正三角形的三棱柱的正视图如图所示,其顶点都在同一个球面上,则该球的内接正方体的表面积为( )
一个底面是正三角形的三棱柱的正视图如图所示,其顶点都在同一个球面上,则该球的内接正方体的表面积为( )| A. | $\frac{19}{6}$ | B. | $\frac{38}{3}$ | C. | $\frac{57}{8}$ | D. | $\frac{19}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com