
 ,
, ],求f(x)的值域.
],求f(x)的值域.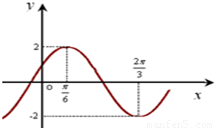
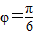 ,从而求得函数的解析式为
,从而求得函数的解析式为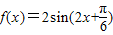 .令
.令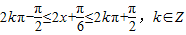 ,求得x的范围,可得以f(x)的增区间.
,求得x的范围,可得以f(x)的增区间.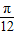 ,
,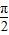 ],根据正弦函数的定义域和值域求得sin(2x+
],根据正弦函数的定义域和值域求得sin(2x+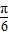 )∈[-
)∈[- ,1],从而得到函数的值域.
,1],从而得到函数的值域.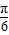 )≥
)≥ ,再由2kπ+
,再由2kπ+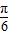 ≤x+
≤x+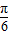 ≤2kπ+
≤2kπ+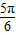 ,k∈z,求得x的范围.
,k∈z,求得x的范围.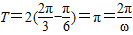 ,∴ω=2.---(3分)
,∴ω=2.---(3分)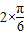 +
+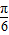 =
=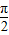 ,∴
,∴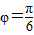 .----------(5分)
.----------(5分)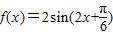 .------(6分)
.------(6分)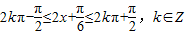 ,---(8分)
,---(8分)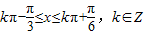 .-----(9分)
.-----(9分)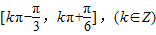 .-------(10分)
.-------(10分)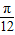 ,
,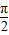 ],可得2x+
],可得2x+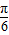 ∈[
∈[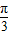 ,
,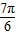 ],∴sin(2x+
],∴sin(2x+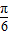 )∈[-
)∈[- ,1],
,1], ,1].
,1].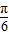 )≥
)≥ ,…(10分)
,…(10分)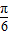 ≤x+
≤x+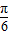 ≤2kπ+
≤2kπ+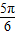 ,k∈z,解得 2kπ≤x≤2kπ+
,k∈z,解得 2kπ≤x≤2kπ+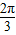 ,k∈z,
,k∈z,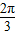 ],k∈z. …(12分)
],k∈z. …(12分)

 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
 已知如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象
已知如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象| π |
| 12 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象.
已知如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象.| π |
| 12 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年新疆乌鲁木齐一中高三(上)第一次月考数学试卷(文科)(解析版) 题型:解答题
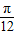 ,
,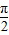 ],求f(x)的值域.
],求f(x)的值域.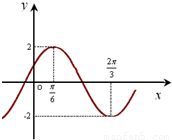
查看答案和解析>>
科目:高中数学 来源:2011-2012学年新疆乌鲁木齐一中高三(上)第一次月考数学试卷(文科)(解析版) 题型:解答题
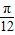 ,
, ],求f(x)的值域.
],求f(x)的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com